Question 1:
Determine the magnitude and direction of the resultant force in the following situations.
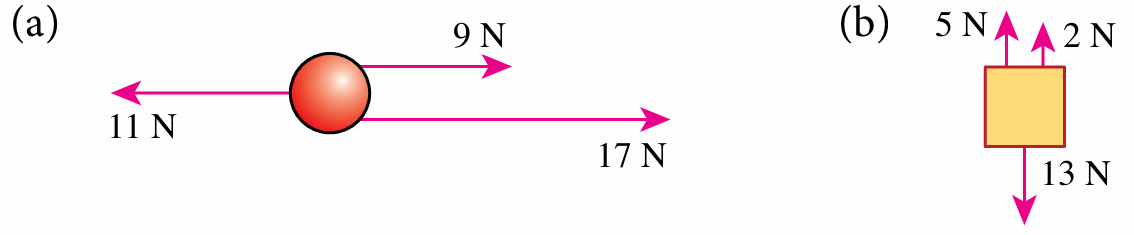
Answer:
(a) Resultant force

(b) Resultant force
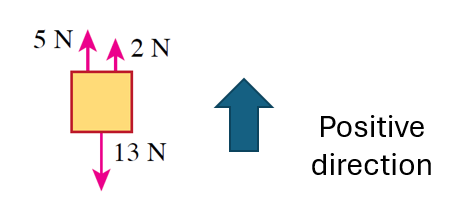

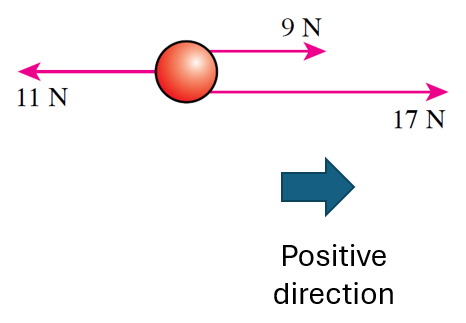
Determine the magnitude and direction of the resultant force in the following situations.

Answer:
(a) Resultant force


(b) Resultant force


Question 2:
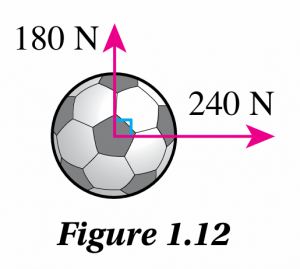
Figure 1.12 shows the forces acting on a ball that is kicked simultaneously by two players.
(a) Sketch a diagram that shows the 240 N force, the 180 N force and the resultant force.
(b) Calculate the magnitude of the resultant force on the ball.
(c) State the direction of motion of the ball.
Answer:
Method 1
(a) By using parallelogram rule
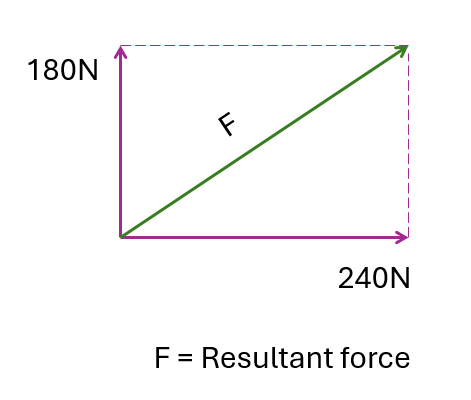
Method 2
(a) By using triangle method
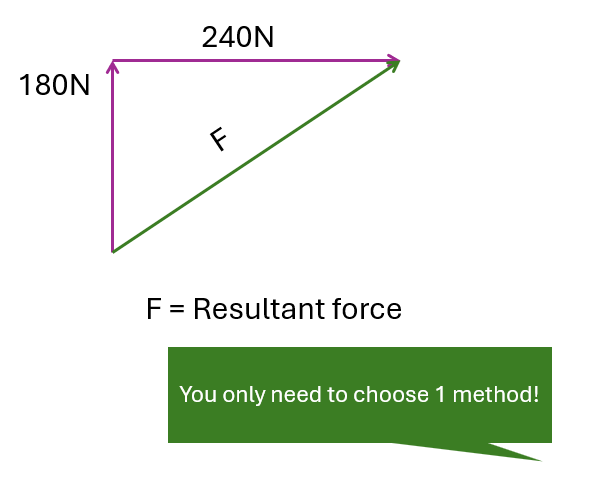
(b) Magnitude of resultant force
$$ \begin{aligned} & |F|=\sqrt{F_1^2+F_2^2} \\ & |F|=\sqrt{180^2+240^2} \\ & |F|=300 \mathrm{~N} \end{aligned} $$
(c) Direction of the resultant force
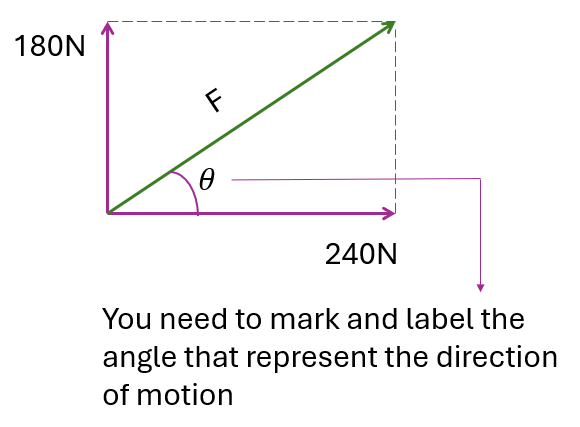
$$ \begin{aligned} & \tan \theta=\frac{180}{240} \\ & \theta=\tan ^{-1} \frac{180}{240} \\ & \theta=36.87^{\circ} \end{aligned} $$

Figure 1.12 shows the forces acting on a ball that is kicked simultaneously by two players.
(a) Sketch a diagram that shows the 240 N force, the 180 N force and the resultant force.
(b) Calculate the magnitude of the resultant force on the ball.
(c) State the direction of motion of the ball.
Answer:
Method 1
(a) By using parallelogram rule

Method 2
(a) By using triangle method

(b) Magnitude of resultant force
$$ \begin{aligned} & |F|=\sqrt{F_1^2+F_2^2} \\ & |F|=\sqrt{180^2+240^2} \\ & |F|=300 \mathrm{~N} \end{aligned} $$
(c) Direction of the resultant force

$$ \begin{aligned} & \tan \theta=\frac{180}{240} \\ & \theta=\tan ^{-1} \frac{180}{240} \\ & \theta=36.87^{\circ} \end{aligned} $$
