Question 3:
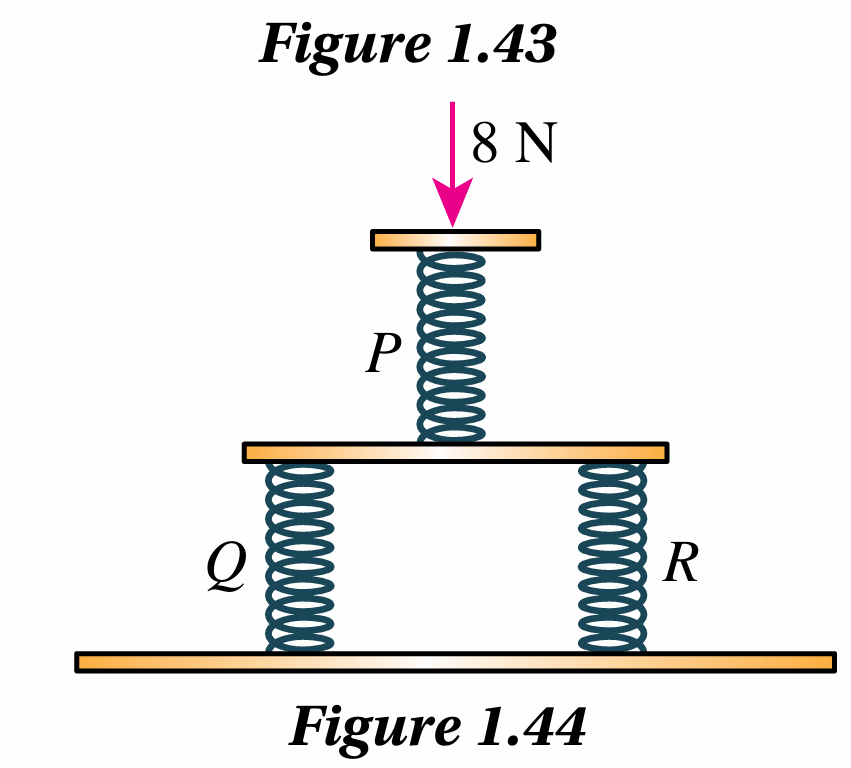
Figure 1.44 shows an arrangement consisting of three identical springs P, Q and R. The spring constant is 4 N cm–1. The arrangement is compressed by an 8 N force. Determine:
(a) the force experienced by each spring
(b) the compression of each spring
(c) the compression of the system of springs
Answer:
(a)
Spring P = 8 N (Spring P hold the 8N force alone fully)
Spring Q = 4 N, Spring R = 4 N (Spring Q and R share the 8N force equally. 8N ÷ 2 = 4N)
(b)
$$ \begin{aligned} & F=k x \text { (Hooke’s Law) } \\ & \text { Compression, } x=\frac{F}{k} \\ & k=4 \mathrm{~N} \mathrm{~cm}^{-1} \end{aligned} $$
$$ \text { Spring } P: \quad x=\frac{8}{4}=2 \mathrm{~cm} $$
$$ \text { Spring } Q: \quad x=\frac{4}{4}=1 \mathrm{~cm} $$
$$ \text { Spring } R: \quad x=1 \mathrm{~cm} $$
(c)
Compression of spring P = 2 cm.
Compression of spring Q and R = 1 cm
Total compression of spring = 2 cm + 1 cm = 3 cm

Figure 1.44 shows an arrangement consisting of three identical springs P, Q and R. The spring constant is 4 N cm–1. The arrangement is compressed by an 8 N force. Determine:
(a) the force experienced by each spring
(b) the compression of each spring
(c) the compression of the system of springs
Answer:
(a)
Spring P = 8 N (Spring P hold the 8N force alone fully)
Spring Q = 4 N, Spring R = 4 N (Spring Q and R share the 8N force equally. 8N ÷ 2 = 4N)
(b)
$$ \begin{aligned} & F=k x \text { (Hooke’s Law) } \\ & \text { Compression, } x=\frac{F}{k} \\ & k=4 \mathrm{~N} \mathrm{~cm}^{-1} \end{aligned} $$
$$ \text { Spring } P: \quad x=\frac{8}{4}=2 \mathrm{~cm} $$
$$ \text { Spring } Q: \quad x=\frac{4}{4}=1 \mathrm{~cm} $$
$$ \text { Spring } R: \quad x=1 \mathrm{~cm} $$
(c)
Compression of spring P = 2 cm.
Compression of spring Q and R = 1 cm
Total compression of spring = 2 cm + 1 cm = 3 cm
Question 4:
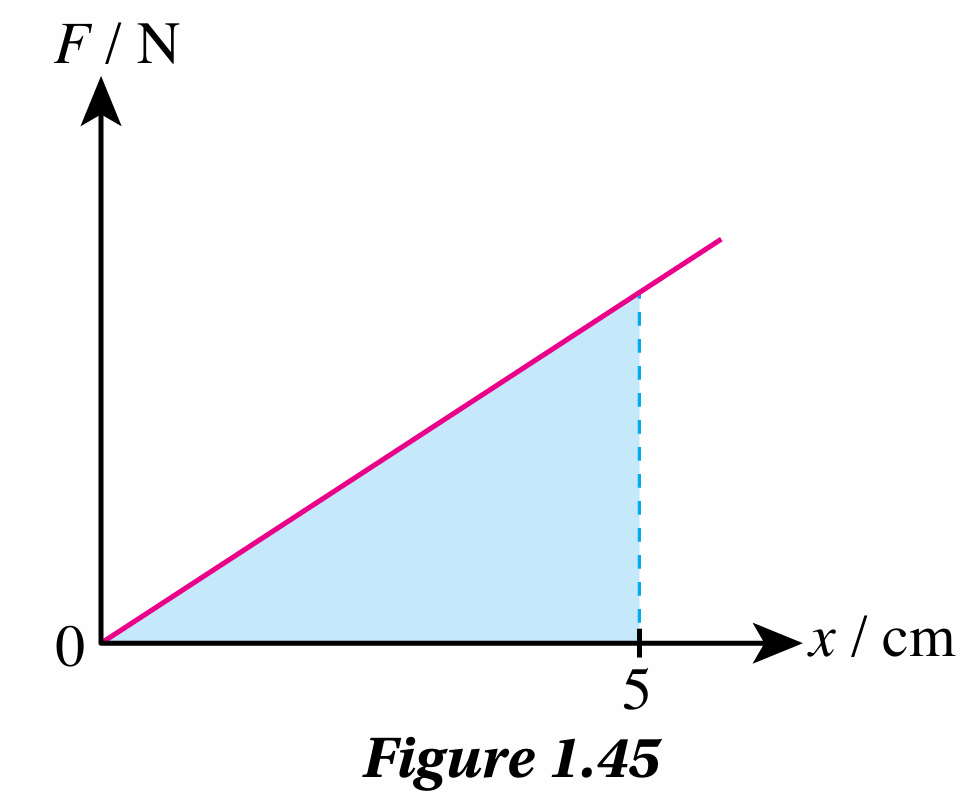
Figure 1.45 shows the graph of F against x for a spring. The shaded area in the graph has a value of 0.4 J.
(a) What is the force that produces the extension of 5 cm in the spring?
(b) Calculate the spring constant.
Answer:
(a)
$$ \text { Extension, } x=5 \mathrm{~cm}=0.05 \mathrm{~m} $$
$$ \begin{aligned} &\text { Elastic potential energy }\\ &E_P=\text { Area of shaded region }=0.4 \mathrm{~J} \end{aligned} $$
$$ \text { Force that produce an extension of } 0.05 \mathrm{~m}=F $$
$$ \begin{aligned} & E_P=\frac{1}{2} F x \\ & 0.4=\frac{1}{2} \times 0.05 \times F \\ & F=16 \mathrm{~N} \end{aligned} $$
(b)
Force, F = 16 N
Extension, x = 0.05 m
$$ \begin{aligned} &F=k x\\ &\begin{aligned} & \text { Spring constant, } k=\frac{F}{x} \\ & =\frac{16}{0.05} \\ & =320 \mathrm{Nm}^{-1} \end{aligned} \end{aligned} $$

Figure 1.45 shows the graph of F against x for a spring. The shaded area in the graph has a value of 0.4 J.
(a) What is the force that produces the extension of 5 cm in the spring?
(b) Calculate the spring constant.
Answer:
(a)
$$ \text { Extension, } x=5 \mathrm{~cm}=0.05 \mathrm{~m} $$
$$ \begin{aligned} &\text { Elastic potential energy }\\ &E_P=\text { Area of shaded region }=0.4 \mathrm{~J} \end{aligned} $$
$$ \text { Force that produce an extension of } 0.05 \mathrm{~m}=F $$
$$ \begin{aligned} & E_P=\frac{1}{2} F x \\ & 0.4=\frac{1}{2} \times 0.05 \times F \\ & F=16 \mathrm{~N} \end{aligned} $$
(b)
Force, F = 16 N
Extension, x = 0.05 m
$$ \begin{aligned} &F=k x\\ &\begin{aligned} & \text { Spring constant, } k=\frac{F}{x} \\ & =\frac{16}{0.05} \\ & =320 \mathrm{Nm}^{-1} \end{aligned} \end{aligned} $$
