Question 1:
Explain the difference between
(a) distance and displacement
(b) speed and velocity
Answer:
(a)
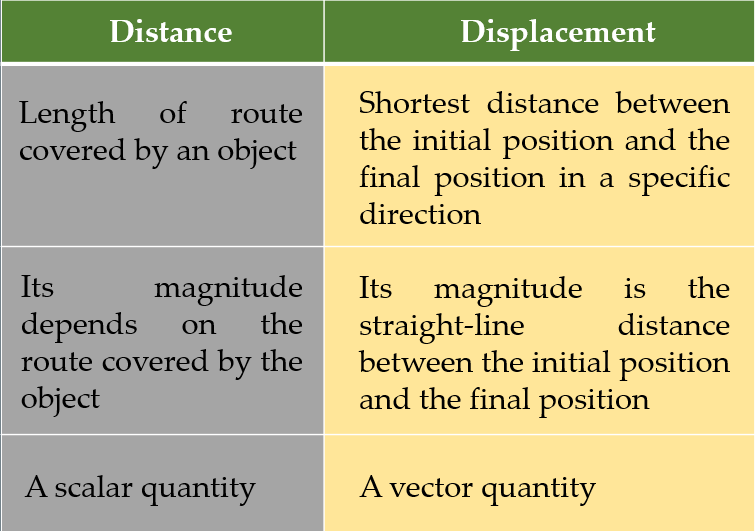
(b)
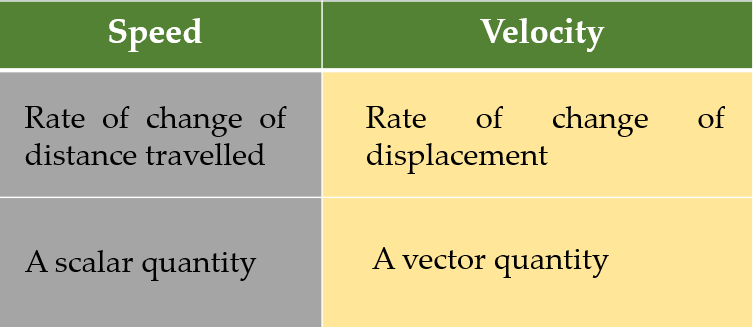
Explain the difference between
(a) distance and displacement
(b) speed and velocity
Answer:
(a)

(b)

Question 2:
A car moving along a straight road at a velocity of 30 m s–1 reduces its velocity at a constant rate until it stops after 5 s. What is the acceleration of the car?
Answer:
$$ \begin{aligned} & u=30 \mathrm{~ms}^{-1} \\ & v=0 \mathrm{~ms}^{-1} \\ & t=5 \mathrm{~s} \\ & a=? \end{aligned} $$
$$ \begin{aligned} a & =\frac{v-u}{t} \\ a & =\frac{0-30}{5} \\ & =-6 \mathrm{~ms}^{-2} \quad \text { (The car decelerates.) } \end{aligned} $$
A car moving along a straight road at a velocity of 30 m s–1 reduces its velocity at a constant rate until it stops after 5 s. What is the acceleration of the car?
Answer:
$$ \begin{aligned} & u=30 \mathrm{~ms}^{-1} \\ & v=0 \mathrm{~ms}^{-1} \\ & t=5 \mathrm{~s} \\ & a=? \end{aligned} $$
$$ \begin{aligned} a & =\frac{v-u}{t} \\ a & =\frac{0-30}{5} \\ & =-6 \mathrm{~ms}^{-2} \quad \text { (The car decelerates.) } \end{aligned} $$
Question 3:
Aina rides a smart personal transporter at the Perdana Botanical Gardens. The transporter accelerates uniformly from a velocity of 1 m s–1 to a velocity of 5 m s–1 in 0.5 minutes.
Calculate the displacement of the transporter.
Answer:
$$ \begin{aligned} & u=1 \mathrm{~ms}^{-1} \\ & v=5 \mathrm{~ms}^{-1} \\ & t=0.5 \text { minute } \\ & s=? \end{aligned} $$
$$ \begin{aligned} s & =\frac{1}{2}(u+v) t \\ s & =\frac{1}{2}(1+5)(0.5 \times 60) \\ & =90 \mathrm{~m} \end{aligned} $$
Aina rides a smart personal transporter at the Perdana Botanical Gardens. The transporter accelerates uniformly from a velocity of 1 m s–1 to a velocity of 5 m s–1 in 0.5 minutes.
Calculate the displacement of the transporter.
Answer:
$$ \begin{aligned} & u=1 \mathrm{~ms}^{-1} \\ & v=5 \mathrm{~ms}^{-1} \\ & t=0.5 \text { minute } \\ & s=? \end{aligned} $$
$$ \begin{aligned} s & =\frac{1}{2}(u+v) t \\ s & =\frac{1}{2}(1+5)(0.5 \times 60) \\ & =90 \mathrm{~m} \end{aligned} $$
