Question 1:
How do you determine
(a) velocity from a graph of displacement against time?
(b) acceleration from a graph of velocity against time?
(c) displacement from a graph of velocity against time?
Answer:
(a) For displacement-time graph:
Velocity = gradient of the graph
(b) For velocity-time graph:
Acceleration = gradient of the graph
(c) For velocity-time graph:
Displacement = area under the graph
How do you determine
(a) velocity from a graph of displacement against time?
(b) acceleration from a graph of velocity against time?
(c) displacement from a graph of velocity against time?
Answer:
(a) For displacement-time graph:
Velocity = gradient of the graph
(b) For velocity-time graph:
Acceleration = gradient of the graph
(c) For velocity-time graph:
Displacement = area under the graph
Question 2:
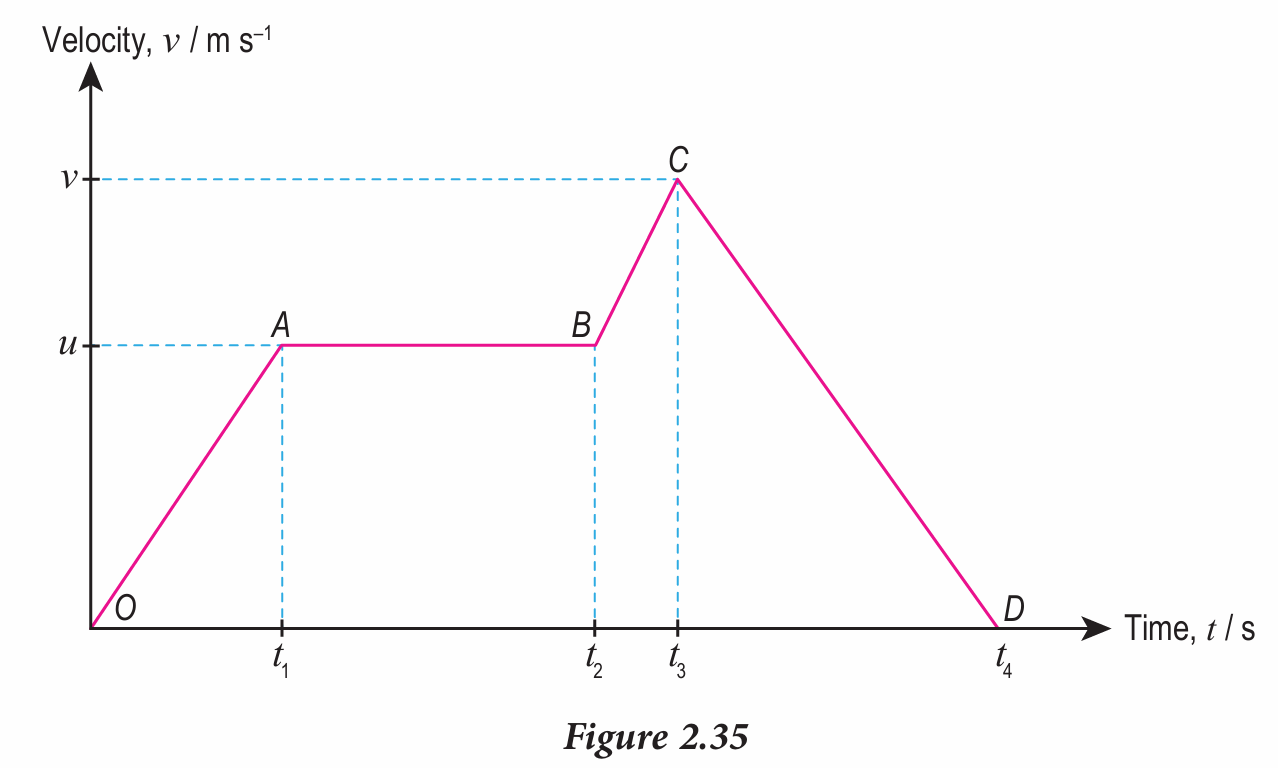
Based on Figure 2.35, describe the motion of the object from O to D.
Answer:
$$ \begin{aligned} &O A \text { (time interval } 0-t_1 \text { ) }\\ &\text { – Moving to the right with a uniform acceleration, } \frac{u-0}{t_1-0} \end{aligned} $$
$$ \left.B C \text { (time interval } t_2-t_3\right) $$
$$ \text { – Moving to the right with acceleration, } \frac{v-u}{t_3-t_2} $$
$$ C D \text { (time interval } t_3-t_4 \text { ) } $$
$$ \text { – Moving to the right with velocity decreases, } $$
$$ \text { acceleration }=\frac{0-v}{t_4-t_3} \text { (deceleration) } $$
Based on Figure 2.35, describe the motion of the object from O to D.

Answer:
$$ \begin{aligned} &O A \text { (time interval } 0-t_1 \text { ) }\\ &\text { – Moving to the right with a uniform acceleration, } \frac{u-0}{t_1-0} \end{aligned} $$
AB (time interval t1 – t2)
– Moving to the right with a uniform velocity, zero acceleration.
$$ \left.B C \text { (time interval } t_2-t_3\right) $$
$$ \text { – Moving to the right with acceleration, } \frac{v-u}{t_3-t_2} $$
$$ C D \text { (time interval } t_3-t_4 \text { ) } $$
$$ \text { – Moving to the right with velocity decreases, } $$
$$ \text { acceleration }=\frac{0-v}{t_4-t_3} \text { (deceleration) } $$
Question 3:
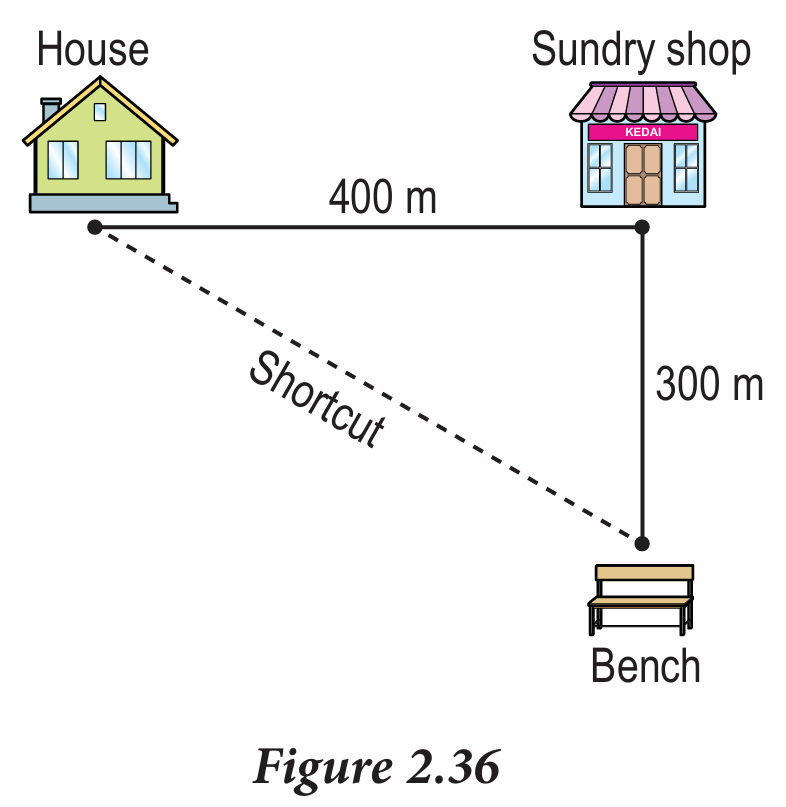
Figure 2.36 shows Rokiah taking 3 minutes to walk to the sundry shop located 400 m to the right of her house. After 1 minute, she buys an ice cream and walks to the playground located 300 m from the sundry shop in 2 minutes. She sits and rests on a bench near the playground for 2 minutes. Then, using a shortcut to return to her house, Rokiah reaches her house in 2 minutes.
(a) What is the average velocity of the motion of Rokiah from
(i) house to the sundry shop?
(ii) sundry shop to the playground?
(iii) playground to the house?
(b) Calculate Rokiah’s average speed.
Answer:
(a)(i)
$$ \begin{aligned} \text { Velocity } & =\frac{\text { Displacement }}{\text { Time taken }} \\ v & =\frac{400}{3 \times 60} \\ & =2.222 \mathrm{~m} / \mathrm{s} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} v & =\frac{300}{2 \times 60} \\ & =2.5 \mathrm{~m} / \mathrm{s} \end{aligned} $$
(a)(iii)
$$ \begin{aligned} \text { Displacement } & =\sqrt{400^2+300^2} \\ & =500 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Velocity } & =\frac{500}{2 \times 60} \\ & =4.17 \mathrm{~m} / \mathrm{s} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Average velocity }=\frac{\text { Total distance }}{\text { Total time taken }} \\ & \qquad \begin{aligned} v & =\frac{400+300+500}{(3+1+2+2+2) \times 60} \\ & =2 \mathrm{~m} / \mathrm{s} \end{aligned} \end{aligned} $$

Figure 2.36 shows Rokiah taking 3 minutes to walk to the sundry shop located 400 m to the right of her house. After 1 minute, she buys an ice cream and walks to the playground located 300 m from the sundry shop in 2 minutes. She sits and rests on a bench near the playground for 2 minutes. Then, using a shortcut to return to her house, Rokiah reaches her house in 2 minutes.
(a) What is the average velocity of the motion of Rokiah from
(i) house to the sundry shop?
(ii) sundry shop to the playground?
(iii) playground to the house?
(b) Calculate Rokiah’s average speed.
Answer:
(a)(i)
$$ \begin{aligned} \text { Velocity } & =\frac{\text { Displacement }}{\text { Time taken }} \\ v & =\frac{400}{3 \times 60} \\ & =2.222 \mathrm{~m} / \mathrm{s} \end{aligned} $$
(a)(ii)
$$ \begin{aligned} v & =\frac{300}{2 \times 60} \\ & =2.5 \mathrm{~m} / \mathrm{s} \end{aligned} $$
(a)(iii)
$$ \begin{aligned} \text { Displacement } & =\sqrt{400^2+300^2} \\ & =500 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} \text { Velocity } & =\frac{500}{2 \times 60} \\ & =4.17 \mathrm{~m} / \mathrm{s} \end{aligned} $$
(b)
$$ \begin{aligned} & \text { Average velocity }=\frac{\text { Total distance }}{\text { Total time taken }} \\ & \qquad \begin{aligned} v & =\frac{400+300+500}{(3+1+2+2+2) \times 60} \\ & =2 \mathrm{~m} / \mathrm{s} \end{aligned} \end{aligned} $$
