Question 4:
A car is driven from rest and accelerated at 4 m s–2 for 8 s along a straight road. Th e car is driven at the constant velocity for 20 s and then its brakes are applied. Th e car reduces its velocity at the rate of 2 m s–2 till it stops. Sketch a graph of:
(a) acceleration against time
(b) velocity against time
(c) displacement against time
Answer:
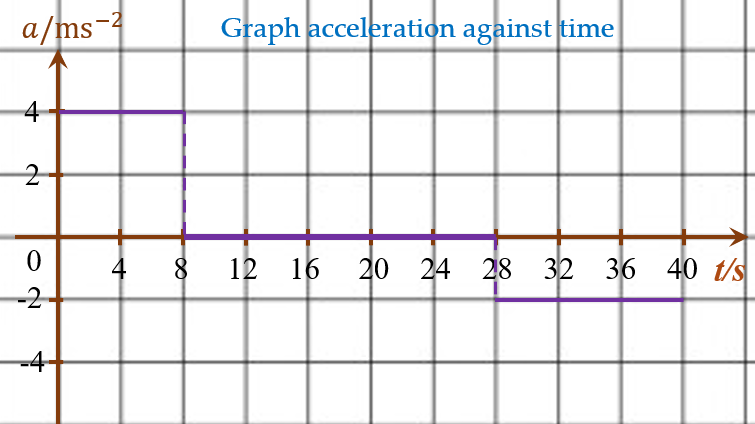
(a)
$$ \text { Stage } 1 \text { – Acceleration at } 4 \mathrm{~ms}^{-2}(8 s) $$
$$ \begin{aligned} &\text { Stage } 2 \text { – Zero acceleration (constant velocity, } 20 \text { s) }\\ &(8+20=28 \mathrm{~s}) \end{aligned} $$
$$ \text { Stage } 3-\text { Deceleration at }-2 \mathrm{~ms}^{-2} \text { till stop. } $$
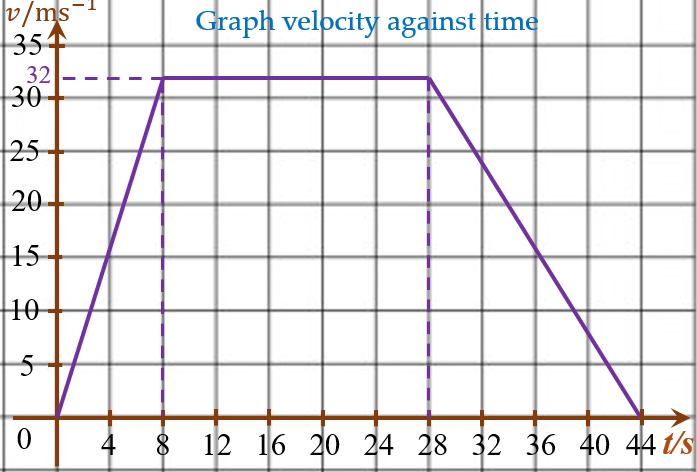
(b)
$$ \begin{aligned} &\text { Stage } 1 \text { (Car accelerates), }\\ &\begin{aligned} a & =4 \mathrm{~ms}^{-2} \\ u & =0 \mathrm{~ms}^{-1} \\ t & =8 \mathrm{~s} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & v=u+a t \\ & v=0+4(8) \\ & v=32 \mathrm{~ms}^{-1} \end{aligned} $$
$$ \text { Stage } 2 \text { (Constant velocity for } 20 \text { s) } $$
$$ \begin{aligned} &\text { Stage } 3 \text { (Car decelerates till stop) }\\ &\begin{aligned} & a=-2 \mathrm{~ms}^{-2} \\ & u=32 \mathrm{~ms}^{-1} \\ & v=0 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & v=u+a t \\ & 0=32+(-2) t \\ & t=16 \mathrm{~s} \end{aligned} $$
$$ \text { Total time }=28+16=44 \mathrm{~s} $$
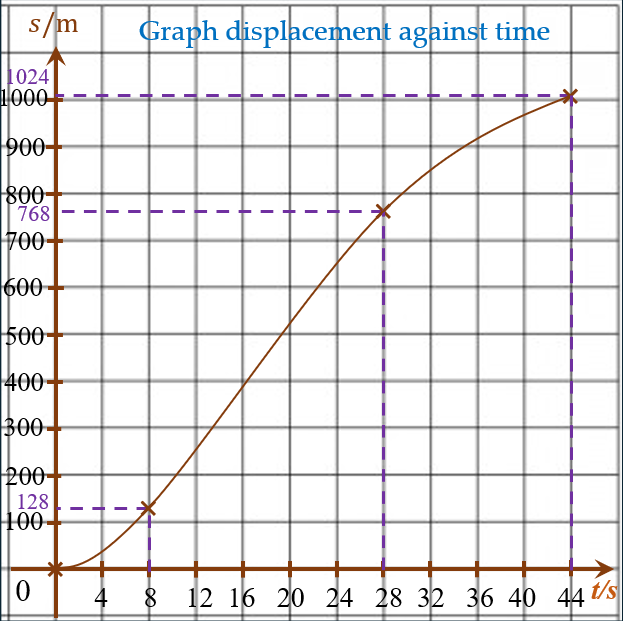
(c)
$$ \begin{aligned} &\text { Stage } 1 \text { (Car accelerates), }\\ &\begin{aligned} a & =4 \mathrm{~ms}^{-2} \\ u & =0 \mathrm{~ms}^{-1} \\ t & =8 \mathrm{~s} \\ s & =? \end{aligned} \end{aligned} $$
$$ \begin{aligned} s & =\frac{1}{2} a t^2 \\ s & =\frac{1}{2}(4)(8)^2 \\ s & =128 \mathrm{~m} \\ s_1 & =128 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} &\text { Stage } 2 \text { (Constant velocity for } 20 \text { s) }\\ &\begin{aligned} u & =v=32 \mathrm{~ms}^{-1} \\ t & =20 \mathrm{~s} \\ s & =? \end{aligned} \end{aligned} $$
$$ \begin{aligned} s & =\frac{1}{2}(u+v) t \\ s & =\frac{1}{2}(32+32)(20) \\ s & =640 \mathrm{~m} \\ s_2 & =128 \mathrm{~m}+640 \mathrm{~m}=768 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} &\text { Stage } 3 \text { (Car decelerates till stop) }\\ &\begin{aligned} u & =32 \mathrm{~ms}^{-1} \\ v & =0 \mathrm{~ms}^{-1} \\ t & =16 s[\text { from (b), 44-28] } \\ s & =? \end{aligned} \end{aligned} $$
$$ \begin{aligned} s & =\frac{1}{2}(u+v) t \\ s & =\frac{1}{2}(32+0)(16) \\ s & =256 \mathrm{~m} \\ s_3 & =768 \mathrm{~m}+256 \mathrm{~m}=1024 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} & t=8 \mathrm{~s}, s_1=128 \mathrm{~m} \\ & t=28 \mathrm{~s}, s_2=768 \mathrm{~m} \\ & t=44 \mathrm{~s}, s_3=1024 \mathrm{~m} \end{aligned} $$
A car is driven from rest and accelerated at 4 m s–2 for 8 s along a straight road. Th e car is driven at the constant velocity for 20 s and then its brakes are applied. Th e car reduces its velocity at the rate of 2 m s–2 till it stops. Sketch a graph of:
(a) acceleration against time
(b) velocity against time
(c) displacement against time
Answer:
(a)
$$ \text { Stage } 1 \text { – Acceleration at } 4 \mathrm{~ms}^{-2}(8 s) $$
$$ \begin{aligned} &\text { Stage } 2 \text { – Zero acceleration (constant velocity, } 20 \text { s) }\\ &(8+20=28 \mathrm{~s}) \end{aligned} $$
$$ \text { Stage } 3-\text { Deceleration at }-2 \mathrm{~ms}^{-2} \text { till stop. } $$

(b)
$$ \begin{aligned} &\text { Stage } 1 \text { (Car accelerates), }\\ &\begin{aligned} a & =4 \mathrm{~ms}^{-2} \\ u & =0 \mathrm{~ms}^{-1} \\ t & =8 \mathrm{~s} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & v=u+a t \\ & v=0+4(8) \\ & v=32 \mathrm{~ms}^{-1} \end{aligned} $$
$$ \text { Stage } 2 \text { (Constant velocity for } 20 \text { s) } $$
$$ \begin{aligned} &\text { Stage } 3 \text { (Car decelerates till stop) }\\ &\begin{aligned} & a=-2 \mathrm{~ms}^{-2} \\ & u=32 \mathrm{~ms}^{-1} \\ & v=0 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & v=u+a t \\ & 0=32+(-2) t \\ & t=16 \mathrm{~s} \end{aligned} $$
$$ \text { Total time }=28+16=44 \mathrm{~s} $$

(c)
$$ \begin{aligned} &\text { Stage } 1 \text { (Car accelerates), }\\ &\begin{aligned} a & =4 \mathrm{~ms}^{-2} \\ u & =0 \mathrm{~ms}^{-1} \\ t & =8 \mathrm{~s} \\ s & =? \end{aligned} \end{aligned} $$
$$ \begin{aligned} s & =\frac{1}{2} a t^2 \\ s & =\frac{1}{2}(4)(8)^2 \\ s & =128 \mathrm{~m} \\ s_1 & =128 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} &\text { Stage } 2 \text { (Constant velocity for } 20 \text { s) }\\ &\begin{aligned} u & =v=32 \mathrm{~ms}^{-1} \\ t & =20 \mathrm{~s} \\ s & =? \end{aligned} \end{aligned} $$
$$ \begin{aligned} s & =\frac{1}{2}(u+v) t \\ s & =\frac{1}{2}(32+32)(20) \\ s & =640 \mathrm{~m} \\ s_2 & =128 \mathrm{~m}+640 \mathrm{~m}=768 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} &\text { Stage } 3 \text { (Car decelerates till stop) }\\ &\begin{aligned} u & =32 \mathrm{~ms}^{-1} \\ v & =0 \mathrm{~ms}^{-1} \\ t & =16 s[\text { from (b), 44-28] } \\ s & =? \end{aligned} \end{aligned} $$
$$ \begin{aligned} s & =\frac{1}{2}(u+v) t \\ s & =\frac{1}{2}(32+0)(16) \\ s & =256 \mathrm{~m} \\ s_3 & =768 \mathrm{~m}+256 \mathrm{~m}=1024 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} & t=8 \mathrm{~s}, s_1=128 \mathrm{~m} \\ & t=28 \mathrm{~s}, s_2=768 \mathrm{~m} \\ & t=44 \mathrm{~s}, s_3=1024 \mathrm{~m} \end{aligned} $$

