Question 7:
Figure 4 shows the reading on a mechanical stopwatch at the start and the end of an experiment. The mechanical stopwatch is used to measure the time taken for 20 complete oscillations of a simple pendulum of length, l.

(a) (i) What is the time taken for the pendulum to make 20 complete oscillations?
(ii) Why is it necessary to take the time for 20 complete oscillations?
(iii) Suggest two ways to improve the experiment.
(b)(i) Determine the period of oscillation, T of this pendulum.
(ii) The relationship between length, l and period, T, of a simple pendulum is given by the equation, l = (g/4π2)T2.
Using the value of T in (b)(i), calculate the length of the pendulum, l.
[g = 10 m s–2]
Answer:
(a)(i) 26 – 2 = 24 s
(a)(ii) To obtain the value of one complete oscillation accurately.
(a)(iii) Step 1: Repeat the experiment and obtain the average value of two sets of readings.
Step 2: Use an electronic or digital stopwatch to measure time more accurately.
(b)(i)
$$ \text { Period } T=\frac{24}{20}=1.2 \mathrm{~s} $$
(b)(ii)
$$ \begin{aligned} l & =10 \div\left(4 \times \pi^2\right) \times 1.2^2 \\ & =0.36 \mathrm{~m} \end{aligned} $$
Figure 4 shows the reading on a mechanical stopwatch at the start and the end of an experiment. The mechanical stopwatch is used to measure the time taken for 20 complete oscillations of a simple pendulum of length, l.

(a) (i) What is the time taken for the pendulum to make 20 complete oscillations?
(ii) Why is it necessary to take the time for 20 complete oscillations?
(iii) Suggest two ways to improve the experiment.
(b)(i) Determine the period of oscillation, T of this pendulum.
(ii) The relationship between length, l and period, T, of a simple pendulum is given by the equation, l = (g/4π2)T2.
Using the value of T in (b)(i), calculate the length of the pendulum, l.
[g = 10 m s–2]
Answer:
(a)(i) 26 – 2 = 24 s
(a)(ii) To obtain the value of one complete oscillation accurately.
(a)(iii) Step 1: Repeat the experiment and obtain the average value of two sets of readings.
Step 2: Use an electronic or digital stopwatch to measure time more accurately.
(b)(i)
$$ \text { Period } T=\frac{24}{20}=1.2 \mathrm{~s} $$
(b)(ii)
$$ \begin{aligned} l & =10 \div\left(4 \times \pi^2\right) \times 1.2^2 \\ & =0.36 \mathrm{~m} \end{aligned} $$
Question 8:
Newton’s Law of Gravitation can be expressed as follows:
$$ F=\frac{G M m}{r^2} $$

(a) Based on the equation, give an example for each of the following:
(i) base quantity
(ii) derived quantity
(iii) vector quantity
(b) Derive the unit of G in terms of S.I. base units.
Answer:
(a)(i) Base quantities – Mass, distance, length
(a)(ii) Derived quantity – Force
(a)(iii) Vector quantity – Force
(b)
$$ \text { S.I. unit for } G=\frac{F r^2}{M m} $$$$ \begin{aligned} & =\frac{\mathrm{kg} \mathrm{~m} \times \mathrm{m}^2}{\mathrm{~s} \times \mathrm{s} \times \mathrm{kg} \times \mathrm{kg}} \\ & =\mathrm{kg}^{-1} \mathrm{~m}^3 \mathrm{~s}^{-2} \end{aligned} $$
Newton’s Law of Gravitation can be expressed as follows:
$$ F=\frac{G M m}{r^2} $$

(a) Based on the equation, give an example for each of the following:
(i) base quantity
(ii) derived quantity
(iii) vector quantity
(b) Derive the unit of G in terms of S.I. base units.
Answer:
(a)(i) Base quantities – Mass, distance, length
(a)(ii) Derived quantity – Force
(a)(iii) Vector quantity – Force
(b)
$$ \text { S.I. unit for } G=\frac{F r^2}{M m} $$$$ \begin{aligned} & =\frac{\mathrm{kg} \mathrm{~m} \times \mathrm{m}^2}{\mathrm{~s} \times \mathrm{s} \times \mathrm{kg} \times \mathrm{kg}} \\ & =\mathrm{kg}^{-1} \mathrm{~m}^3 \mathrm{~s}^{-2} \end{aligned} $$
Question 9:
A driver wants to know the petrol consumption per km of a car in a journey of 300 km at constant speed. He installed a measuring device to record the remaining volume of petrol at every 50 km interval from the starting point. Table 4 shows the readings obtained.
(a) The driver forgot to record the volume of petrol at the starting point of the journey.
How can the driver estimate the volume of petrol at the start of the journey?
(b) Determine the petrol consumption of the car for the first 80 km. Show how you obtain the answer.
(c) If the petrol consumption of the car for every 50 km travelled can be saved by 10%, show the new values of V for every corresponding s in a table.
(d) Plot a graph of the new V against s.
Answer:
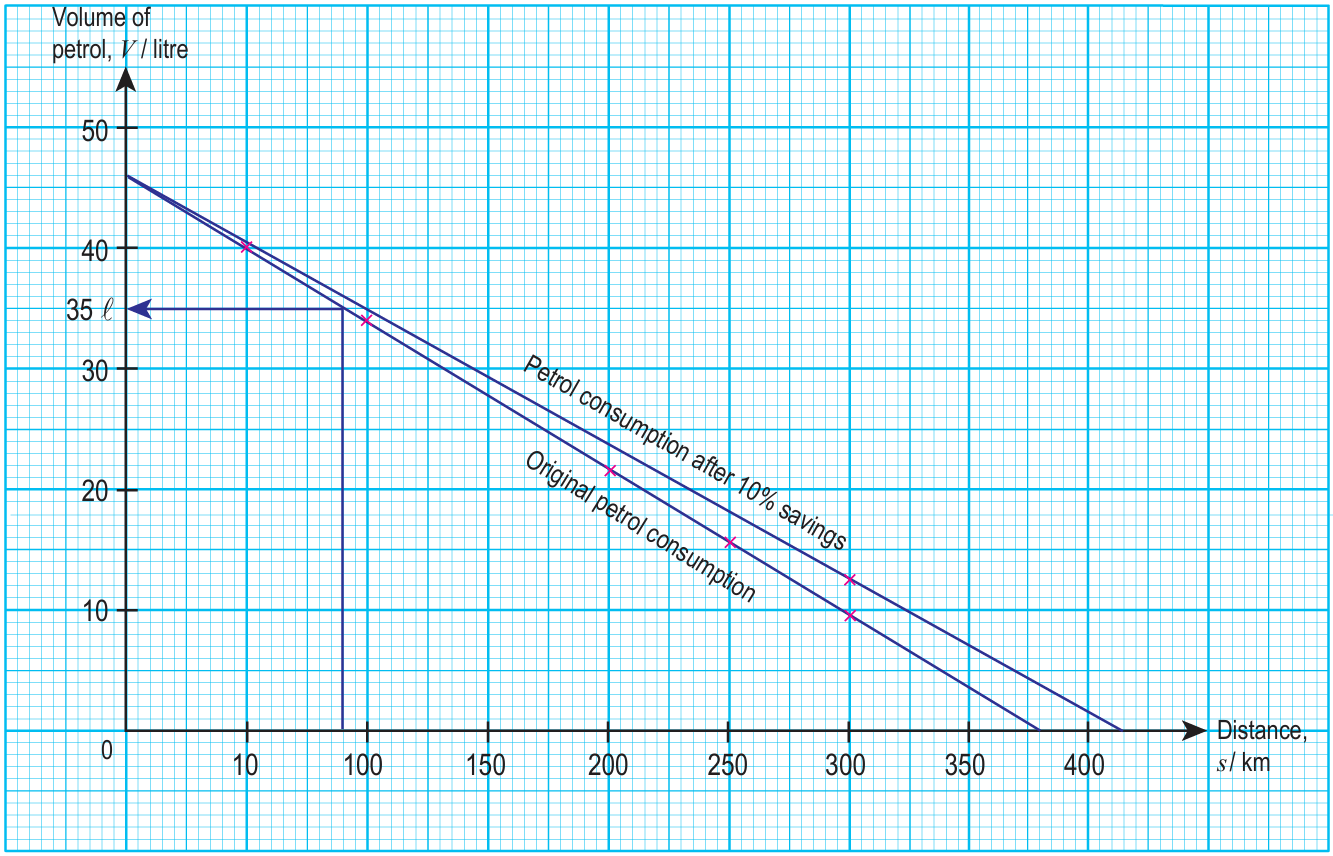
(a) Draw a graph of V against s and extrapolate the graph to a distance, s = 0 km, V = 46 l
(b) – Draw an interpolated line at s = 80 km, read the value for V = 35 l
– Consumption of petrol by engine for the first 80 km is 46 l – 35 l = 11 l
(c)

(d)
A driver wants to know the petrol consumption per km of a car in a journey of 300 km at constant speed. He installed a measuring device to record the remaining volume of petrol at every 50 km interval from the starting point. Table 4 shows the readings obtained.

(a) The driver forgot to record the volume of petrol at the starting point of the journey.
How can the driver estimate the volume of petrol at the start of the journey?
(b) Determine the petrol consumption of the car for the first 80 km. Show how you obtain the answer.
(c) If the petrol consumption of the car for every 50 km travelled can be saved by 10%, show the new values of V for every corresponding s in a table.
(d) Plot a graph of the new V against s.
Answer:
(a) Draw a graph of V against s and extrapolate the graph to a distance, s = 0 km, V = 46 l
(b) – Draw an interpolated line at s = 80 km, read the value for V = 35 l
– Consumption of petrol by engine for the first 80 km is 46 l – 35 l = 11 l
(c)

(d)

