Question 10:
Figure 7 shows the graph of force against extension for steel spring M and steel spring N.
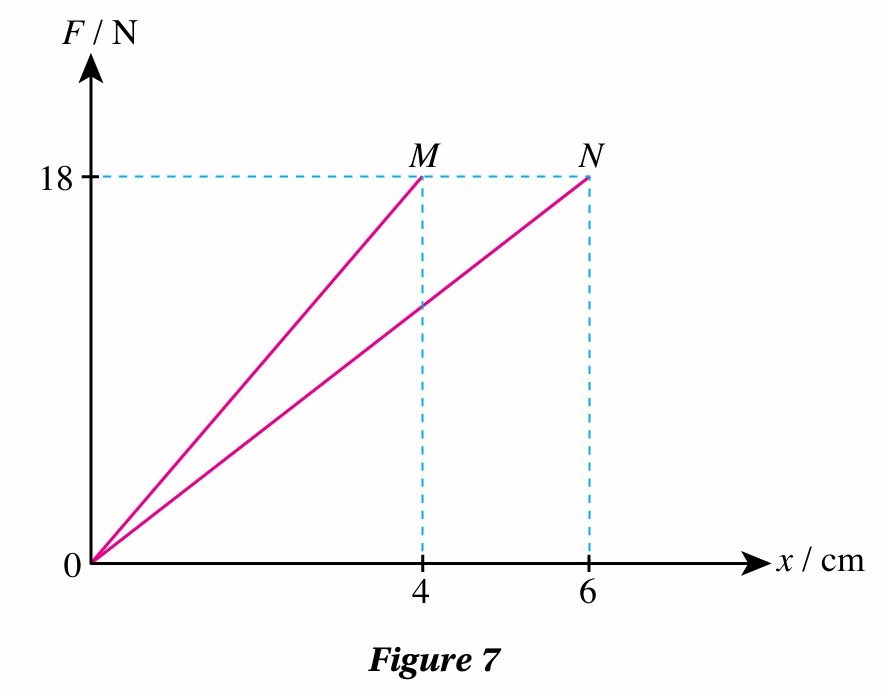
(a) Calculate the spring constant for steel spring M.
(b) What is the elastic potential energy stored in steel spring N when it is stretched to an extension of 6 cm?
(c) Compare and contrast steel spring M with steel spring N.
Answer:
(a)
Spring M : force F = 18 N produces an extension, x = 4 cm = 0.04 m
$$ \text { Spring constant of spring } \begin{aligned} M & =\frac{18}{0.04} \\ & =450 \mathrm{~N} \mathrm{~m}^{-1} \end{aligned} $$
(b)
Spring N: extension, x
= 6 cm
= 0.06 m
$$ \begin{aligned} \text { Elastic potential energy } & =\frac{1}{2} \times 0.06 \times 18 \\ & =0.54 \mathrm{~J} \end{aligned} $$
(c)
The graph for both springs are straight lines passing through the origin.
Both springs obey Hooke’s law.
Spring N obeys Hooke’s law to a greater extension than spring M.
Gradient of graph M > gradient of graph N
Spring constant M > spring constant N
Spring M is stiffer than spring N.
When an 18 N force is applied, the area under the graph N is larger than the area under the graph M.
Spring N stores more elastic potential energy than spring M when both springs are stretched by the same force.
Figure 7 shows the graph of force against extension for steel spring M and steel spring N.

(a) Calculate the spring constant for steel spring M.
(b) What is the elastic potential energy stored in steel spring N when it is stretched to an extension of 6 cm?
(c) Compare and contrast steel spring M with steel spring N.
Answer:
(a)
Spring M : force F = 18 N produces an extension, x = 4 cm = 0.04 m
$$ \text { Spring constant of spring } \begin{aligned} M & =\frac{18}{0.04} \\ & =450 \mathrm{~N} \mathrm{~m}^{-1} \end{aligned} $$
(b)
Spring N: extension, x
= 6 cm
= 0.06 m
$$ \begin{aligned} \text { Elastic potential energy } & =\frac{1}{2} \times 0.06 \times 18 \\ & =0.54 \mathrm{~J} \end{aligned} $$
(c)
The graph for both springs are straight lines passing through the origin.
Both springs obey Hooke’s law.
Spring N obeys Hooke’s law to a greater extension than spring M.
Gradient of graph M > gradient of graph N
Spring constant M > spring constant N
Spring M is stiffer than spring N.
When an 18 N force is applied, the area under the graph N is larger than the area under the graph M.
Spring N stores more elastic potential energy than spring M when both springs are stretched by the same force.
Question 11:
A spring stores elastic potential energy of 18 J when the extension of the spring is 4.0 cm.
What is the force required to stretch the spring to an extension of 3.0 cm?
Answer:
Elastic potential energy, EP = 18 J
Extension of spring, x = 4.0 cm = 0.04 m
$$ \begin{aligned} E_{\mathrm{P}} & =\frac{1}{2} k x^2 \\ \frac{1}{2} \times k \times 0.04^2 & =18 \\ k & =22500 \mathrm{~N} \mathrm{~m}^{-1} \end{aligned} $$
$$ \text { When } \begin{aligned} x & =3.0 \mathrm{~cm} \\ & =0.03 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} F & =k x \\ & =22500 \times 0.03 \\ & =675 \mathrm{~N} \end{aligned} $$
A spring stores elastic potential energy of 18 J when the extension of the spring is 4.0 cm.
What is the force required to stretch the spring to an extension of 3.0 cm?
Answer:
Elastic potential energy, EP = 18 J
Extension of spring, x = 4.0 cm = 0.04 m
$$ \begin{aligned} E_{\mathrm{P}} & =\frac{1}{2} k x^2 \\ \frac{1}{2} \times k \times 0.04^2 & =18 \\ k & =22500 \mathrm{~N} \mathrm{~m}^{-1} \end{aligned} $$
$$ \text { When } \begin{aligned} x & =3.0 \mathrm{~cm} \\ & =0.03 \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} F & =k x \\ & =22500 \times 0.03 \\ & =675 \mathrm{~N} \end{aligned} $$
