Question 1:
(a) State seven base quantities and their S.I. units.
(b) Power, P can be defi ned using the formula,
$$ P=\frac{\text { Force × Length }}{\text { Time }} $$
Derive the unit for P in terms of S.I. base units.
Answer:
(a)

(b) kg m2 s-3
(a) State seven base quantities and their S.I. units.
(b) Power, P can be defi ned using the formula,
$$ P=\frac{\text { Force × Length }}{\text { Time }} $$
Derive the unit for P in terms of S.I. base units.
Answer:
(a)

(b) kg m2 s-3
Question 2:
Figure 1 shows a graph of speed, v against time, t obtained from the speed test of a car.
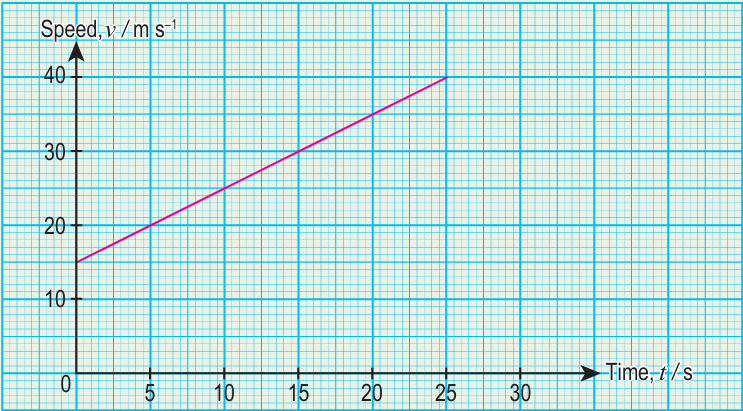
(a) Determine the gradient of the graph v against t.
(b) Determine the y-intercept of the graph when t = 0.
(c) State the relationship between speed, v and time, t.
Answer:
(a) gradient of graph = 1 m s–2
(b) y-intercept of the graph when t = 0 is 15 m s–1
(c) v increases linearly with t
Figure 1 shows a graph of speed, v against time, t obtained from the speed test of a car.

(a) Determine the gradient of the graph v against t.
(b) Determine the y-intercept of the graph when t = 0.
(c) State the relationship between speed, v and time, t.
Answer:
(a) gradient of graph = 1 m s–2
(b) y-intercept of the graph when t = 0 is 15 m s–1
(c) v increases linearly with t
Question 3:
Hashim carried out an experiment to investigate the relationship between the mass of slotted weights and the period of oscillation, T of a spring as shown in Figure 2.
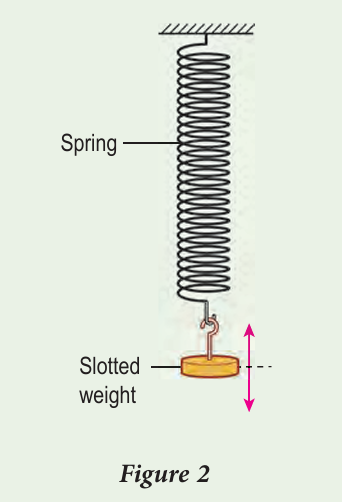
Hashim measured the time, t for 20 complete oscillations for different masses of slotted weights. The data obtained is shown in Table 1.
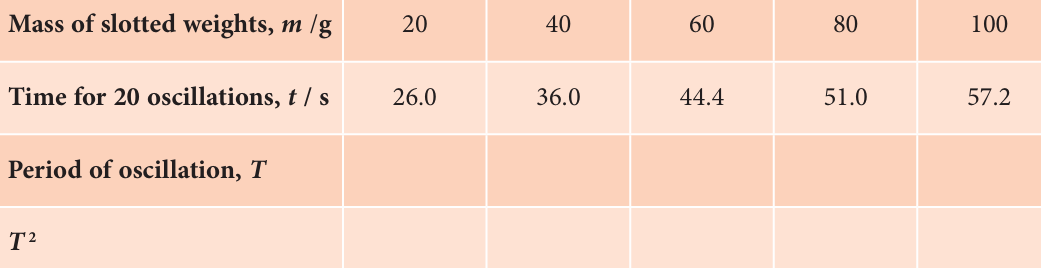
(a) Complete Table 1 by calculating the values of derived data T and T2. State the appropriate units for both the physical quantities.
(b) Plot a graph of T2 against m with appropriate scales. Draw the best fit line.
(c) Determine the gradient of the graph. Show clearly how it is done.
(d) If the experiment is done on the Moon, what is likely to happen to the gradient of the graph?
(e) How can an oscillating spring with slotted weights be used as a time measuring device with unit of measurement in seconds?
$$ \left(T^2=4 \pi^2 \frac{m}{k}\right) $$
Answer:
(a)

(b)
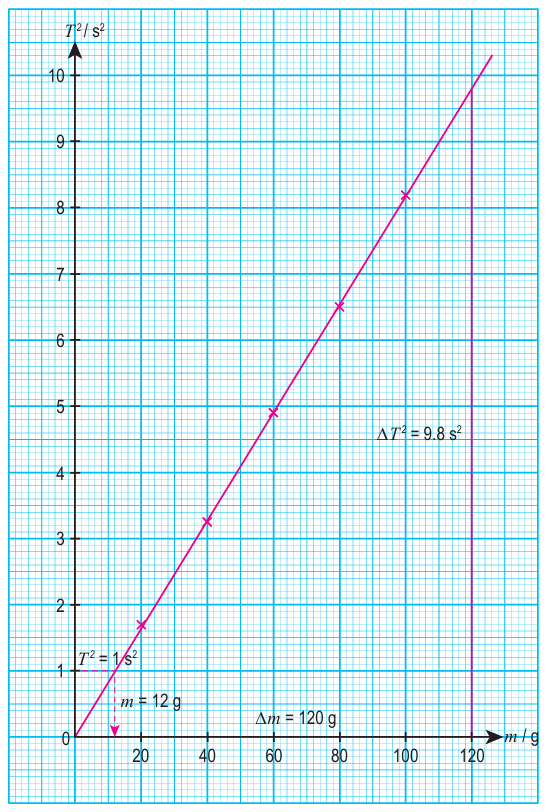
(c) 0.0817 s2 g–1
(d) Unchanged because the period of oscillation of a loaded spring does not depend on the value of the gravitational acceleration.
(e) From the graph of T2 against m, use the method of extrapolation to determine the value of m when T2 = 1.0 s, so T is equal to 1.0 s. Substitute the slotted weights with plasticine of mass m, about 12 g.
Hashim carried out an experiment to investigate the relationship between the mass of slotted weights and the period of oscillation, T of a spring as shown in Figure 2.

Hashim measured the time, t for 20 complete oscillations for different masses of slotted weights. The data obtained is shown in Table 1.

(a) Complete Table 1 by calculating the values of derived data T and T2. State the appropriate units for both the physical quantities.
(b) Plot a graph of T2 against m with appropriate scales. Draw the best fit line.
(c) Determine the gradient of the graph. Show clearly how it is done.
(d) If the experiment is done on the Moon, what is likely to happen to the gradient of the graph?
(e) How can an oscillating spring with slotted weights be used as a time measuring device with unit of measurement in seconds?
$$ \left(T^2=4 \pi^2 \frac{m}{k}\right) $$
Answer:
(a)

(b)

(c) 0.0817 s2 g–1
(d) Unchanged because the period of oscillation of a loaded spring does not depend on the value of the gravitational acceleration.
(e) From the graph of T2 against m, use the method of extrapolation to determine the value of m when T2 = 1.0 s, so T is equal to 1.0 s. Substitute the slotted weights with plasticine of mass m, about 12 g.
