Question 6:
Figure 5 shows a wooden block with a bar magnet tied to it sliding with an acceleration down a smooth track.
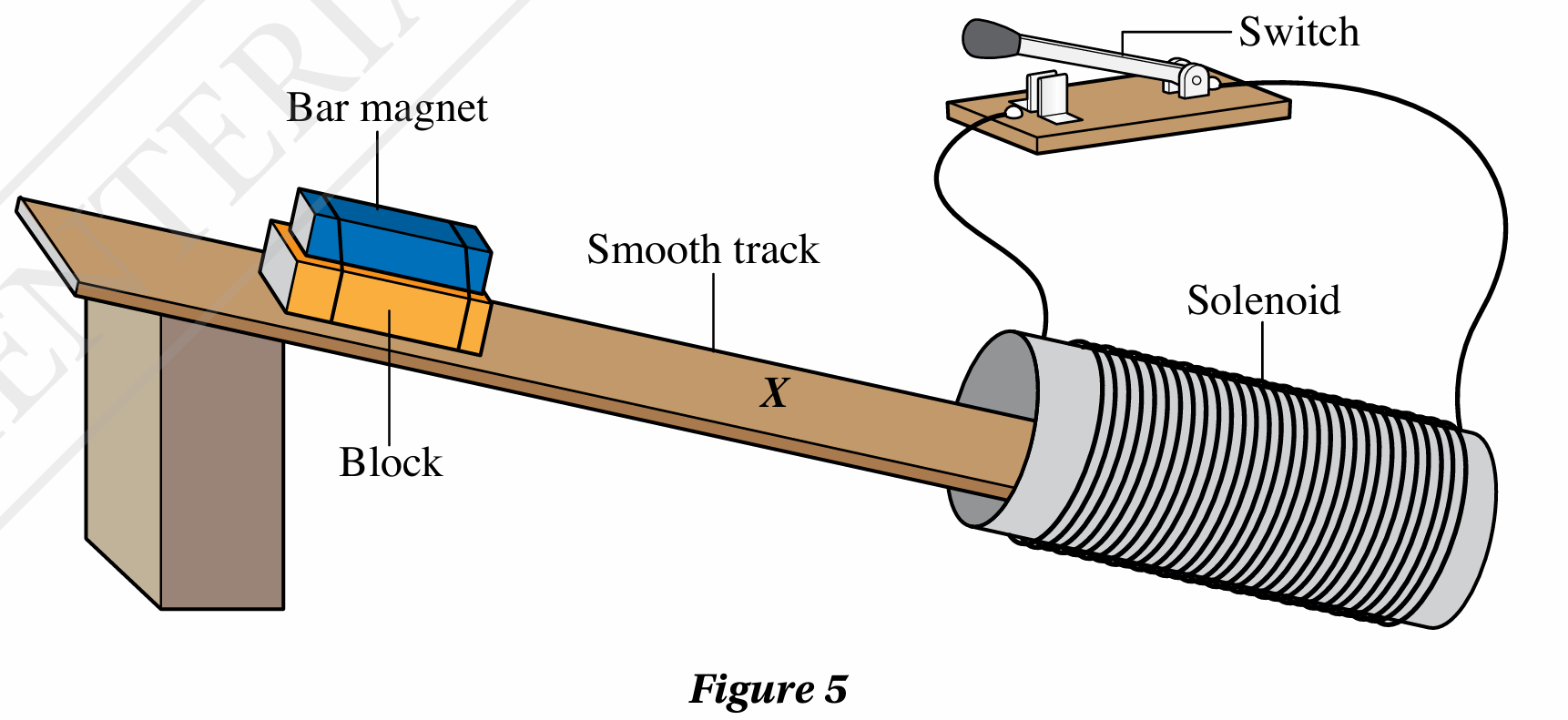
When the block arrives at mark X on the track, the switch is turned on.
(a) What is produced in the solenoid? Explain your answer.
(b) Explain the motion of the block after the switch is turned on.
(c) Based on your answers in 6(a) and (b), discuss the effectiveness of electromagnetic braking in stopping a moving object.
Answer:
(a)
Induced current is produced in the solenoid.
The motion of the bar magnet towards the solenoid causes the cutting of magnetic field lines by the solenoid.
An e.m.f. is induced across the solenoid.
When the switch is turned on, the induced e.m.f. produces an induced current in the solenoid.
(b)
The motion of the block will experience a deceleration.
According to Lenz’s law, the induced current produces a magnetic pole at the end of the solenoid that is the same as the pole of the bar magnet so that the motion of the bar magnet is opposed.
(c)
Electromagnetic braking is more effective than braking that uses frictional force.
– does not need human action to activate the braking process
– does not need electric power to produce a braking force
– the magnitude of the braking force is controlled by factors such as the strength of the magnet and number of turns of the solenoid, that is factors that can be fixed during the construction of the system.
Figure 5 shows a wooden block with a bar magnet tied to it sliding with an acceleration down a smooth track.
When the block arrives at mark X on the track, the switch is turned on.
(a) What is produced in the solenoid? Explain your answer.
(b) Explain the motion of the block after the switch is turned on.
(c) Based on your answers in 6(a) and (b), discuss the effectiveness of electromagnetic braking in stopping a moving object.
Answer:
(a)
Induced current is produced in the solenoid.
The motion of the bar magnet towards the solenoid causes the cutting of magnetic field lines by the solenoid.
An e.m.f. is induced across the solenoid.
When the switch is turned on, the induced e.m.f. produces an induced current in the solenoid.
(b)
The motion of the block will experience a deceleration.
According to Lenz’s law, the induced current produces a magnetic pole at the end of the solenoid that is the same as the pole of the bar magnet so that the motion of the bar magnet is opposed.
(c)
Electromagnetic braking is more effective than braking that uses frictional force.
– does not need human action to activate the braking process
– does not need electric power to produce a braking force
– the magnitude of the braking force is controlled by factors such as the strength of the magnet and number of turns of the solenoid, that is factors that can be fixed during the construction of the system.
Question 7:
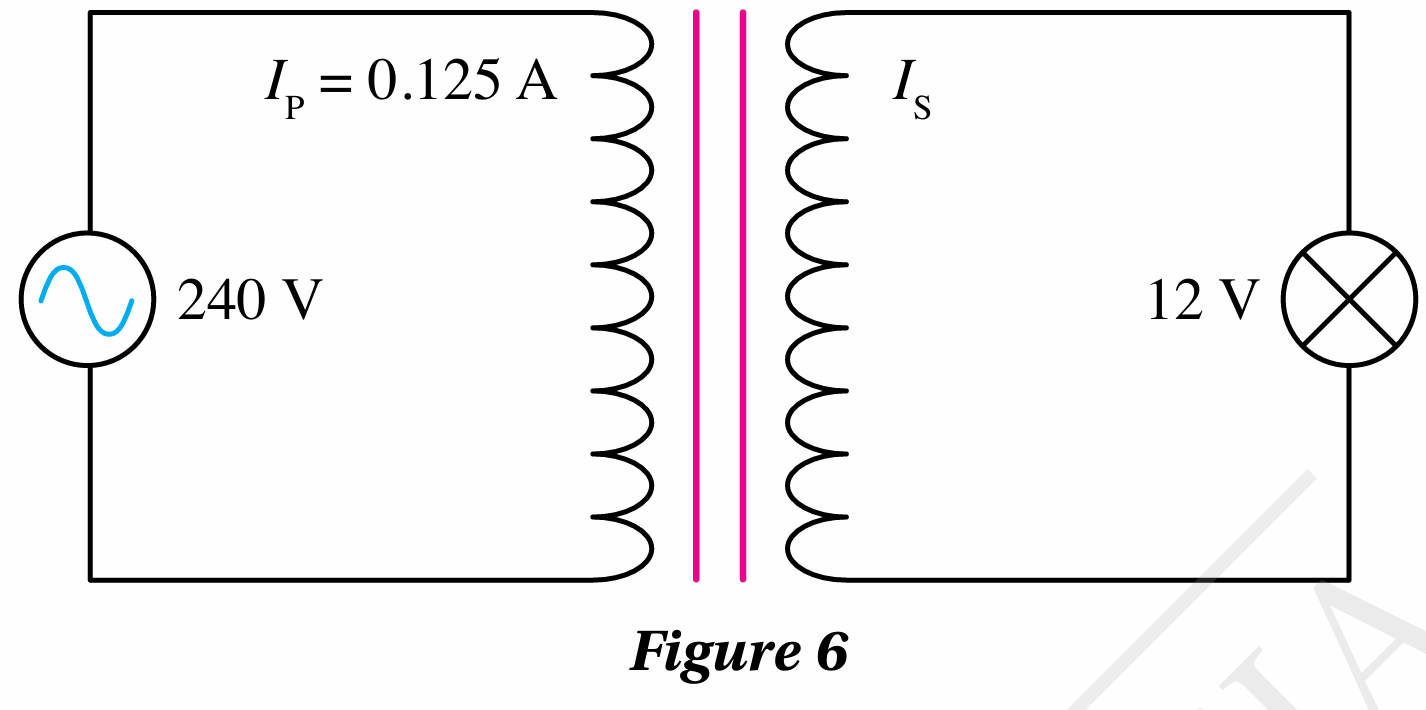Figure 6 shows a transformer with a bulb at its output terminals.
(a) Calculate the value of IS.
(b) What assumption needs to be made in your calculation in 7(a)?
Answer:
(a)
$$ \begin{aligned} V_{\mathrm{S}} I_{\mathrm{S}} & =V_{\mathrm{P}} I_{\mathrm{P}} \\ 12 \times I_{\mathrm{S}} & =240 \times 0.125 \\ I_{\mathrm{S}} & =\frac{240 \times 0.125}{12} \\ I_{\mathrm{S}} & =2.5 \mathrm{~A} \end{aligned} $$
(b) The transformer is ideal
Figure 6 shows a transformer with a bulb at its output terminals. (a) Calculate the value of IS.
(b) What assumption needs to be made in your calculation in 7(a)?
Answer:
(a)
$$ \begin{aligned} V_{\mathrm{S}} I_{\mathrm{S}} & =V_{\mathrm{P}} I_{\mathrm{P}} \\ 12 \times I_{\mathrm{S}} & =240 \times 0.125 \\ I_{\mathrm{S}} & =\frac{240 \times 0.125}{12} \\ I_{\mathrm{S}} & =2.5 \mathrm{~A} \end{aligned} $$
(b) The transformer is ideal
Question 8:
A pupil investigated the operation of a transformer and gathered data as shown in Figure 7. Calculate the efficiency of the transformer and suggest improvements to the design of the transformer to increase its efficiency.
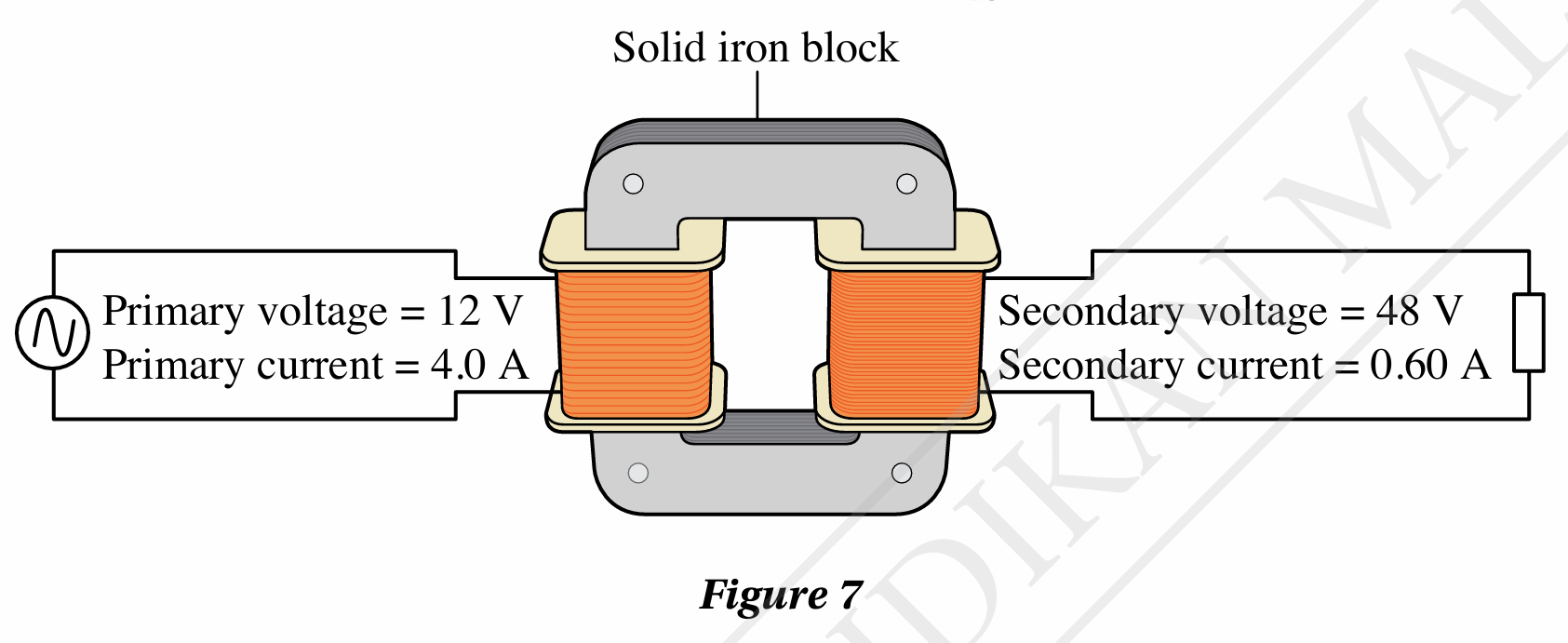
Answer:
Efficiency,
$$ \begin{aligned} \eta & =\frac{\text { Output power }}{\text { Input power }} \times 100 \% \\ & =\frac{V_{\mathrm{s}} I_{\mathrm{s}}}{V_{\mathrm{P}} I_{\mathrm{P}}} \times 100 \% \\ & =\frac{48 \times 0.6}{12 \times 4.0} \times 100 \% \\ & =60.00 \% \end{aligned} $$
A pupil investigated the operation of a transformer and gathered data as shown in Figure 7. Calculate the efficiency of the transformer and suggest improvements to the design of the transformer to increase its efficiency.
Answer:
Efficiency,
$$ \begin{aligned} \eta & =\frac{\text { Output power }}{\text { Input power }} \times 100 \% \\ & =\frac{V_{\mathrm{s}} I_{\mathrm{s}}}{V_{\mathrm{P}} I_{\mathrm{P}}} \times 100 \% \\ & =\frac{48 \times 0.6}{12 \times 4.0} \times 100 \% \\ & =60.00 \% \end{aligned} $$
– Use laminated soft iron core
– The secondary coil is wound on top of the primary coil