Question 12:
A technician was assigned to study the use of three types of springs, X, Y and Z with spring constants given in Table 1.
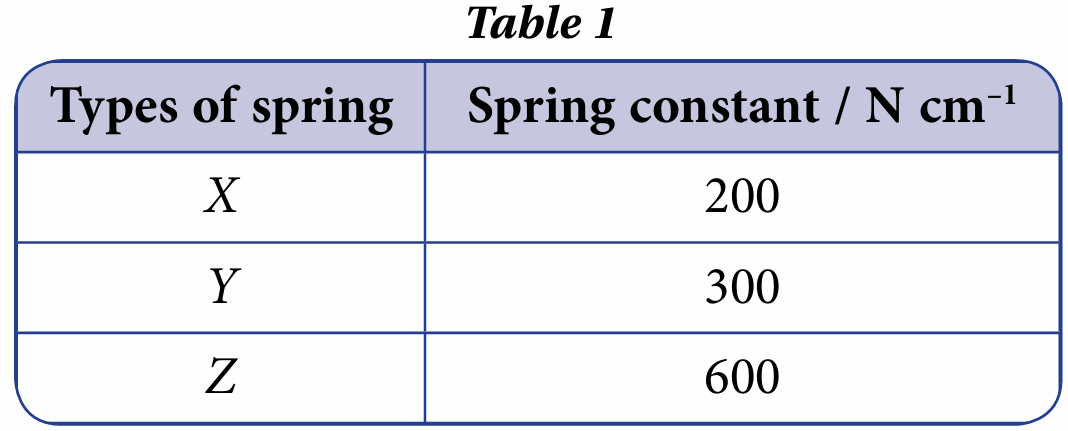
(a) Table 2 shows four arrangements of springs considered by the technician.
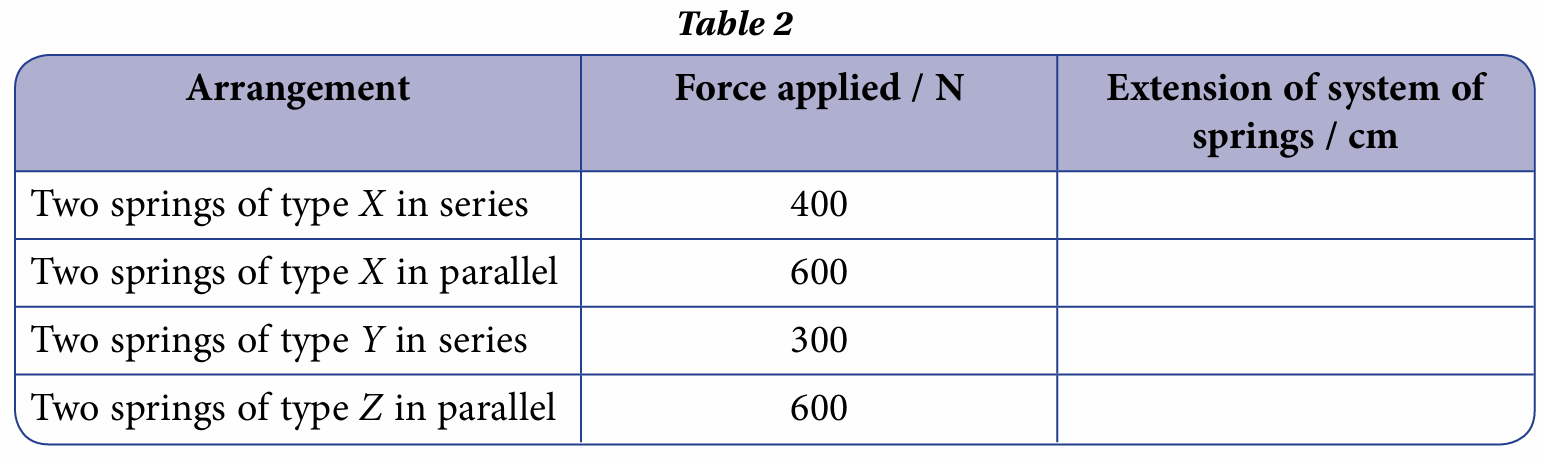
For each arrangement of springs, determine the extension and complete Table 2.
(b) What is the assumption that you have made based on your calculation in 12(a)?
Answer:
(a) The extension of a spring is calculated as follows:
$$ \begin{aligned} & F=k x \\ & \text { Extension, } x=\frac{F}{k} \end{aligned} $$
(b) Each spring obeys Hooke’s law.
A technician was assigned to study the use of three types of springs, X, Y and Z with spring constants given in Table 1.

(a) Table 2 shows four arrangements of springs considered by the technician.

For each arrangement of springs, determine the extension and complete Table 2.
(b) What is the assumption that you have made based on your calculation in 12(a)?
Answer:
(a) The extension of a spring is calculated as follows:
$$ \begin{aligned} & F=k x \\ & \text { Extension, } x=\frac{F}{k} \end{aligned} $$

(b) Each spring obeys Hooke’s law.
Question 13:
Figure 8 shows an iron plate on the floor of a warehouse.
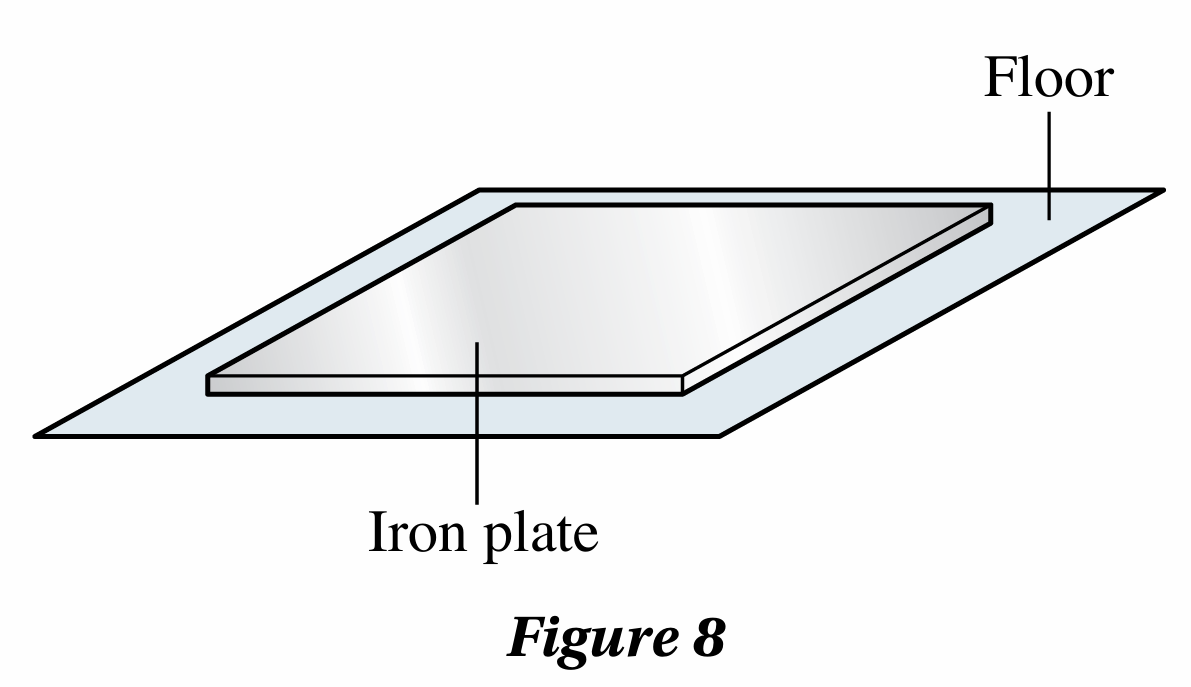
The iron plate is to be supported by a system of springs below it. The system of springs is capable of supporting a maximum load of 3 600 kg with a compression of 5.0 cm.
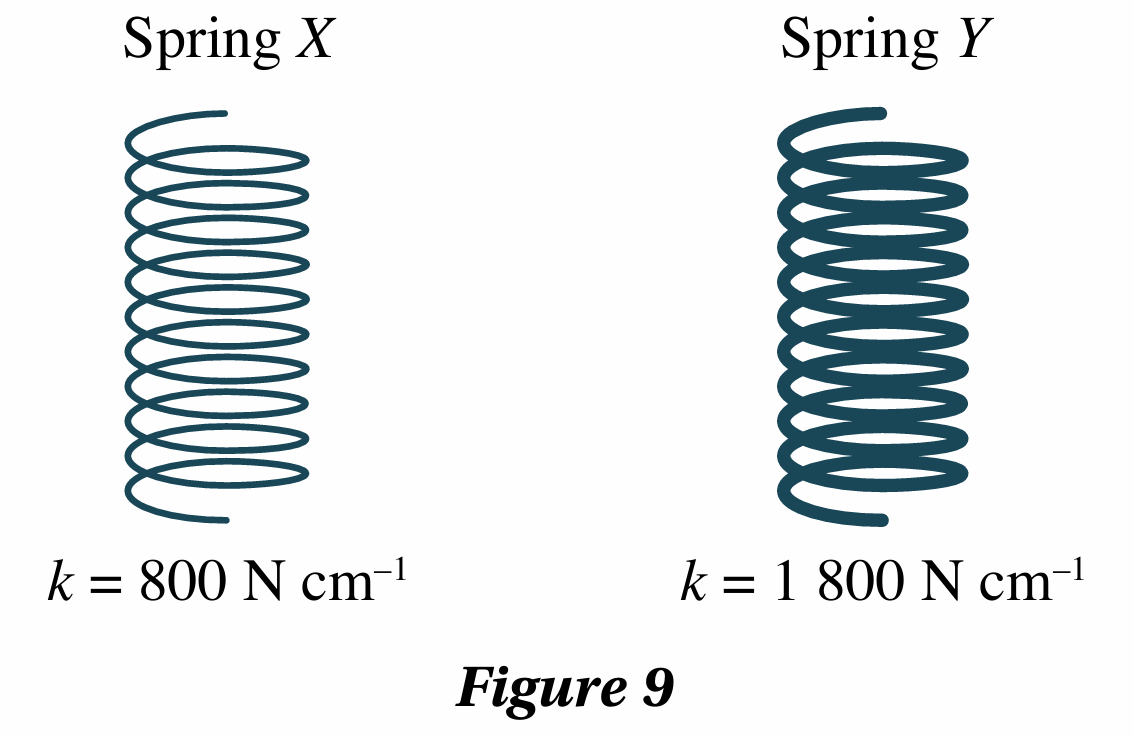
Figure 9 shows two types of springs that can be used.
You are given the task of suggesting a suitable design for the system of springs to support the iron plate.
Your suggestion should consider the following aspects:
(a) the type of spring used
(b) the number of springs used
(c) the position of each spring
Justify the design that you have suggested.
[Gravitational acceleration, g = 9.81 m s–2]
Answer:
Maximum weight of load
= 3 600 × 9.81
= 35 316 N
Let the number of springs be arranged in parallel below the iron plate = n
$$ \text { Compression force on each spring, } F=\frac{35316}{n} $$
$$ \begin{aligned} & \text { From } F=k x, k=\text { spring constant } \\ & x=\text { compression of spring } \end{aligned} $$
$$ \begin{aligned} \frac{35316}{n} & =k x \\ n & =\frac{35316}{k x} \end{aligned} $$
$$ \begin{aligned} &\text { If spring } X \text { is used, } k=800 \mathrm{~N} \mathrm{~cm}^{-1}, x=5.0 \mathrm{~cm}\\ &\begin{aligned} n & =\frac{35316}{800 \times 5} \\ & =8.829 \\ & \approx 9 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { If spring } Y \text { is used, } k=1800 \mathrm{~N} \mathrm{~cm}^{-1}, x=5.0 \mathrm{~cm}\\ &\begin{aligned} n & =\frac{35316}{1800 \times 5} \\ & =3.924 \\ & \approx 4 \end{aligned} \end{aligned} $$
The maximum load will produce a compression of 5.0 cm when 9 springs X are arranged in parallel or 4 springs Y are arranged in parallel.
Suggested design of spring system:
(a) Spring X is used.
– Spring X has a smaller spring constant. More springs X are required.
(b) 9 spring X are arranged in parallel below the iron plate.
– The maximum load is divided into nine smaller components, that is 4 000 N on each spring.
(c) The 9 spring X are placed at positions numbered 1 to 9.
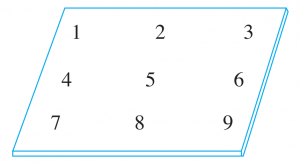
– The uniform distribution of springs ensures that the iron plate is supported in a balanced and stable condition.
Figure 8 shows an iron plate on the floor of a warehouse.

The iron plate is to be supported by a system of springs below it. The system of springs is capable of supporting a maximum load of 3 600 kg with a compression of 5.0 cm.
Figure 9 shows two types of springs that can be used.

You are given the task of suggesting a suitable design for the system of springs to support the iron plate.
Your suggestion should consider the following aspects:
(a) the type of spring used
(b) the number of springs used
(c) the position of each spring
Justify the design that you have suggested.
[Gravitational acceleration, g = 9.81 m s–2]
Answer:
Maximum weight of load
= 3 600 × 9.81
= 35 316 N
Let the number of springs be arranged in parallel below the iron plate = n
$$ \text { Compression force on each spring, } F=\frac{35316}{n} $$
$$ \begin{aligned} & \text { From } F=k x, k=\text { spring constant } \\ & x=\text { compression of spring } \end{aligned} $$
$$ \begin{aligned} \frac{35316}{n} & =k x \\ n & =\frac{35316}{k x} \end{aligned} $$
$$ \begin{aligned} &\text { If spring } X \text { is used, } k=800 \mathrm{~N} \mathrm{~cm}^{-1}, x=5.0 \mathrm{~cm}\\ &\begin{aligned} n & =\frac{35316}{800 \times 5} \\ & =8.829 \\ & \approx 9 \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { If spring } Y \text { is used, } k=1800 \mathrm{~N} \mathrm{~cm}^{-1}, x=5.0 \mathrm{~cm}\\ &\begin{aligned} n & =\frac{35316}{1800 \times 5} \\ & =3.924 \\ & \approx 4 \end{aligned} \end{aligned} $$
The maximum load will produce a compression of 5.0 cm when 9 springs X are arranged in parallel or 4 springs Y are arranged in parallel.
Suggested design of spring system:
(a) Spring X is used.
– Spring X has a smaller spring constant. More springs X are required.
(b) 9 spring X are arranged in parallel below the iron plate.
– The maximum load is divided into nine smaller components, that is 4 000 N on each spring.
(c) The 9 spring X are placed at positions numbered 1 to 9.

– The uniform distribution of springs ensures that the iron plate is supported in a balanced and stable condition.
