Question 4:
Justify the following statement.

Answer:
The resultant force of the two forces has the largest magnitude when the forces act on an object in the same direction.
If the force 17 N and the force 13 N are in the same direction, resultant force
= 17 + 13
= 30 N
The resultant force of the two forces has the smallest magnitude when the forces are in opposite directions.
If the force 17 N and the force 13 N are in opposite directions, resultant force
= 17 + (–13)
= 4 N
Therefore, the resultant forces of 17 N and 13 N has magnitude between 4 N and 30 N.
Justify the following statement.

Answer:
The resultant force of the two forces has the largest magnitude when the forces act on an object in the same direction.
If the force 17 N and the force 13 N are in the same direction, resultant force
= 17 + 13
= 30 N
The resultant force of the two forces has the smallest magnitude when the forces are in opposite directions.
If the force 17 N and the force 13 N are in opposite directions, resultant force
= 17 + (–13)
= 4 N
Therefore, the resultant forces of 17 N and 13 N has magnitude between 4 N and 30 N.
Question 5:
The motion of a motorcycle of mass 180 kg is as follows.

For each stage, state the magnitude and direction of the resultant force on the motorcycle.
Answer:
Stage I: For a stationary object, velocity = 0 and acceleration, a = 0.
Resultant force, F = ma
F = 0 N
Stage II: u = 0, v = 20 m s-1, t = 8 s
$$ \begin{aligned} &\text { Acceleration, }\\ &\begin{aligned} a & =\frac{20-0}{8} \\ & =2.5 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Resultant force, }\\ &\begin{aligned} F & =180 \times 2.5 \\ & =450 \mathrm{~N} \text { to the East } \end{aligned} \end{aligned} $$
Stage III: For an object moving with a uniform velocity, acceleration, a = 0.
Resultant force, F = ma
F = 0 N
The motion of a motorcycle of mass 180 kg is as follows.

For each stage, state the magnitude and direction of the resultant force on the motorcycle.
Answer:
Stage I: For a stationary object, velocity = 0 and acceleration, a = 0.
Resultant force, F = ma
F = 0 N
Stage II: u = 0, v = 20 m s-1, t = 8 s
$$ \begin{aligned} &\text { Acceleration, }\\ &\begin{aligned} a & =\frac{20-0}{8} \\ & =2.5 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Resultant force, }\\ &\begin{aligned} F & =180 \times 2.5 \\ & =450 \mathrm{~N} \text { to the East } \end{aligned} \end{aligned} $$
Stage III: For an object moving with a uniform velocity, acceleration, a = 0.
Resultant force, F = ma
F = 0 N
Question 6:
Figure 4 shows a chef exerting a force of 12 N to cut an onion.
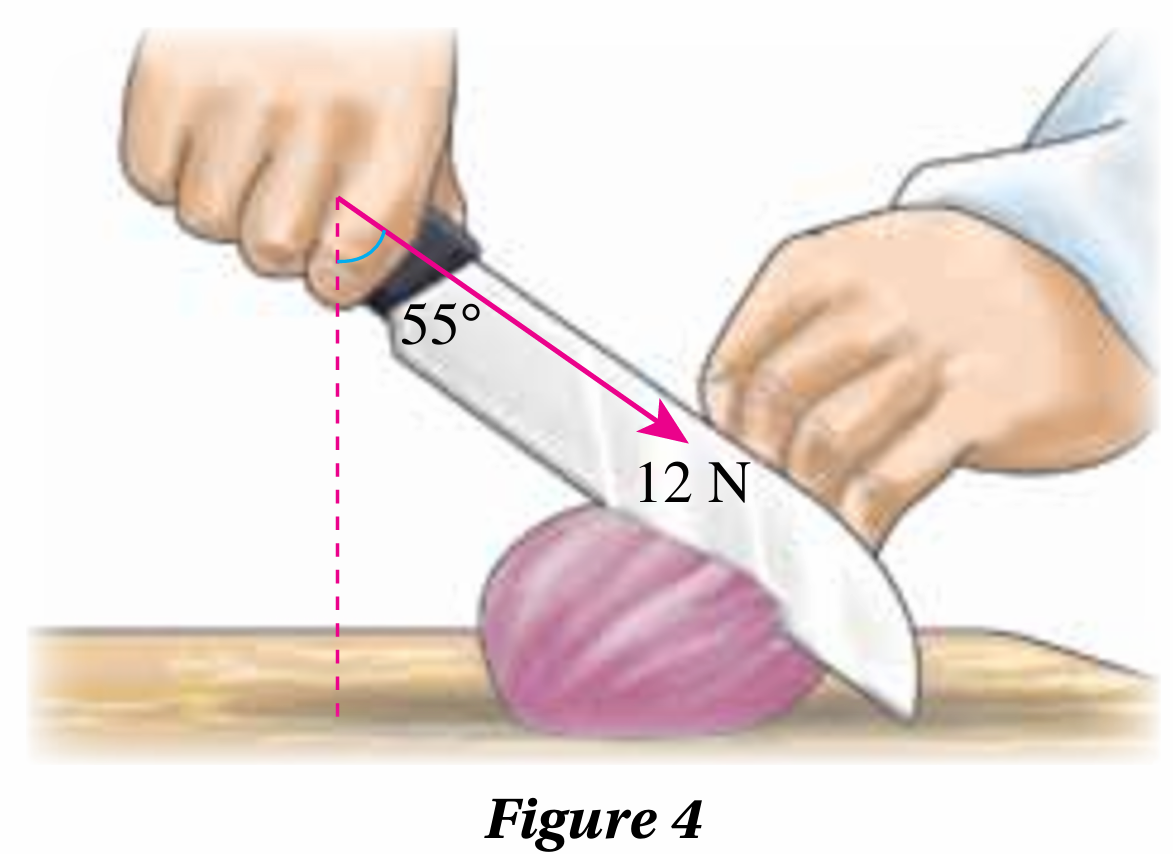
(a) Calculate the horizontal component and vertical component of the 12 N force.
(b) What is the function of the horizontal component and vertical component in the action of cutting the onion?
Answer:
(a)
$$ \begin{aligned} \text { Horizontal component } & =12 \sin 55^{\circ} \\ & =9.83 \mathrm{~N} \\ \text { Vertical component } & =12 \cos 55^{\circ} \\ & =6.88 \mathrm{~N} \end{aligned} $$
(b) The horizontal component moves the knife forward.
The vertical component pushes the knife downward.
Figure 4 shows a chef exerting a force of 12 N to cut an onion.

(a) Calculate the horizontal component and vertical component of the 12 N force.
(b) What is the function of the horizontal component and vertical component in the action of cutting the onion?
Answer:
(a)
$$ \begin{aligned} \text { Horizontal component } & =12 \sin 55^{\circ} \\ & =9.83 \mathrm{~N} \\ \text { Vertical component } & =12 \cos 55^{\circ} \\ & =6.88 \mathrm{~N} \end{aligned} $$
(b) The horizontal component moves the knife forward.
The vertical component pushes the knife downward.
