Question 7:
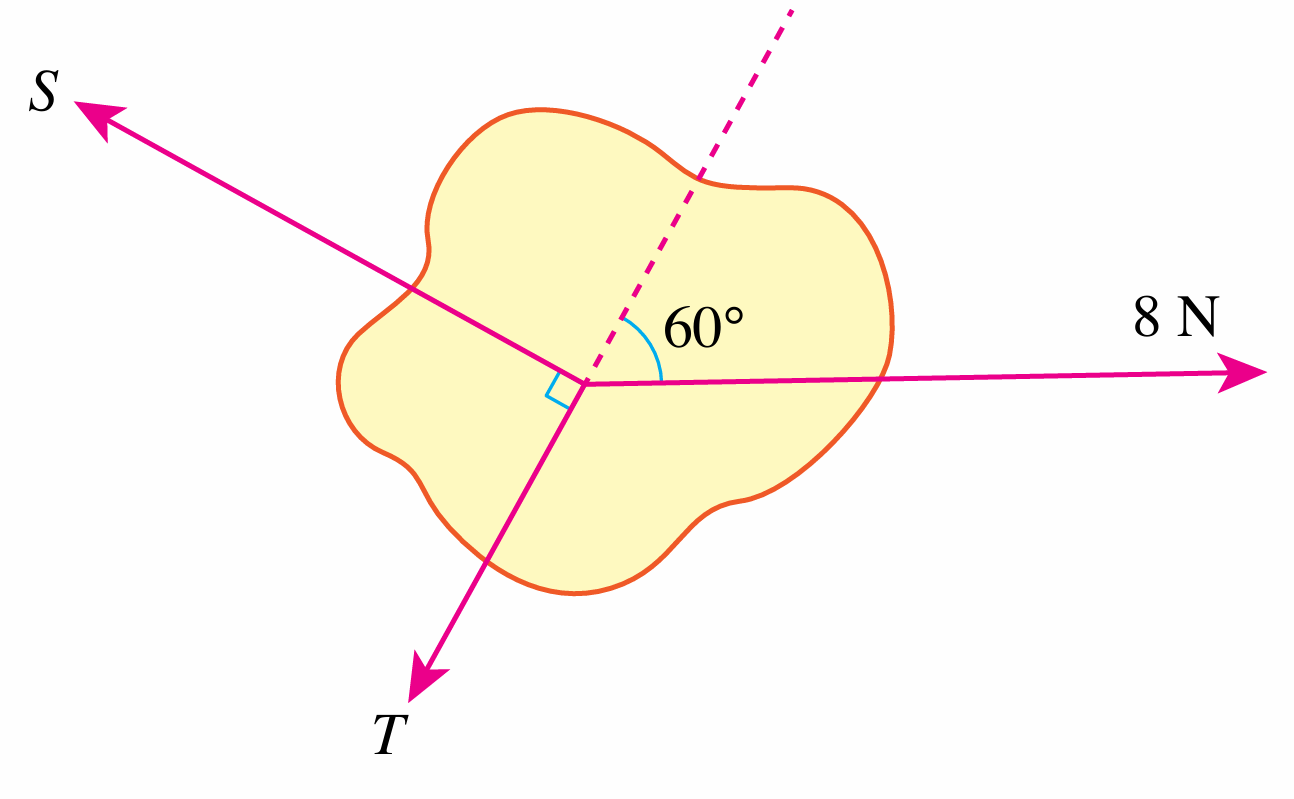
Figure 5 shows three forces acting on an object. The object is at rest. Calculate the magnitude of forces S and T.
Answer:
Three forces S, T and 8 N form a triangle when drawn in sequence.
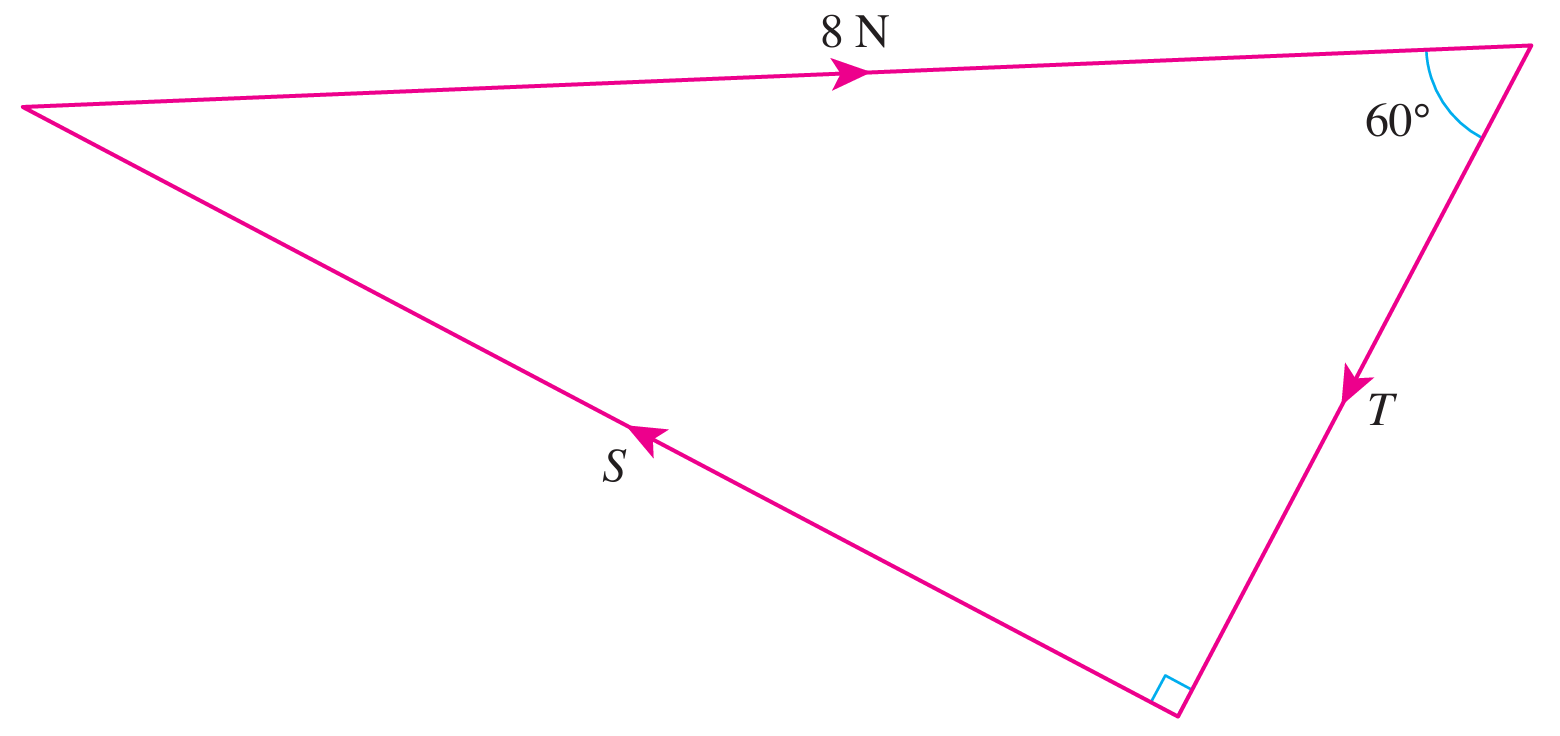
$$ \begin{aligned} \frac{T}{8} & =\cos 60^{\circ} \\ T & =8 \cos 60^{\circ} \\ & =4.0 \mathrm{~N} \\ S & =\sqrt{8^2-4^2} \\ & =6.93 \mathrm{~N} \end{aligned} $$
Figure 5 shows three forces acting on an object. The object is at rest. Calculate the magnitude of forces S and T.

Answer:
Three forces S, T and 8 N form a triangle when drawn in sequence.

$$ \begin{aligned} \frac{T}{8} & =\cos 60^{\circ} \\ T & =8 \cos 60^{\circ} \\ & =4.0 \mathrm{~N} \\ S & =\sqrt{8^2-4^2} \\ & =6.93 \mathrm{~N} \end{aligned} $$
Question 8:
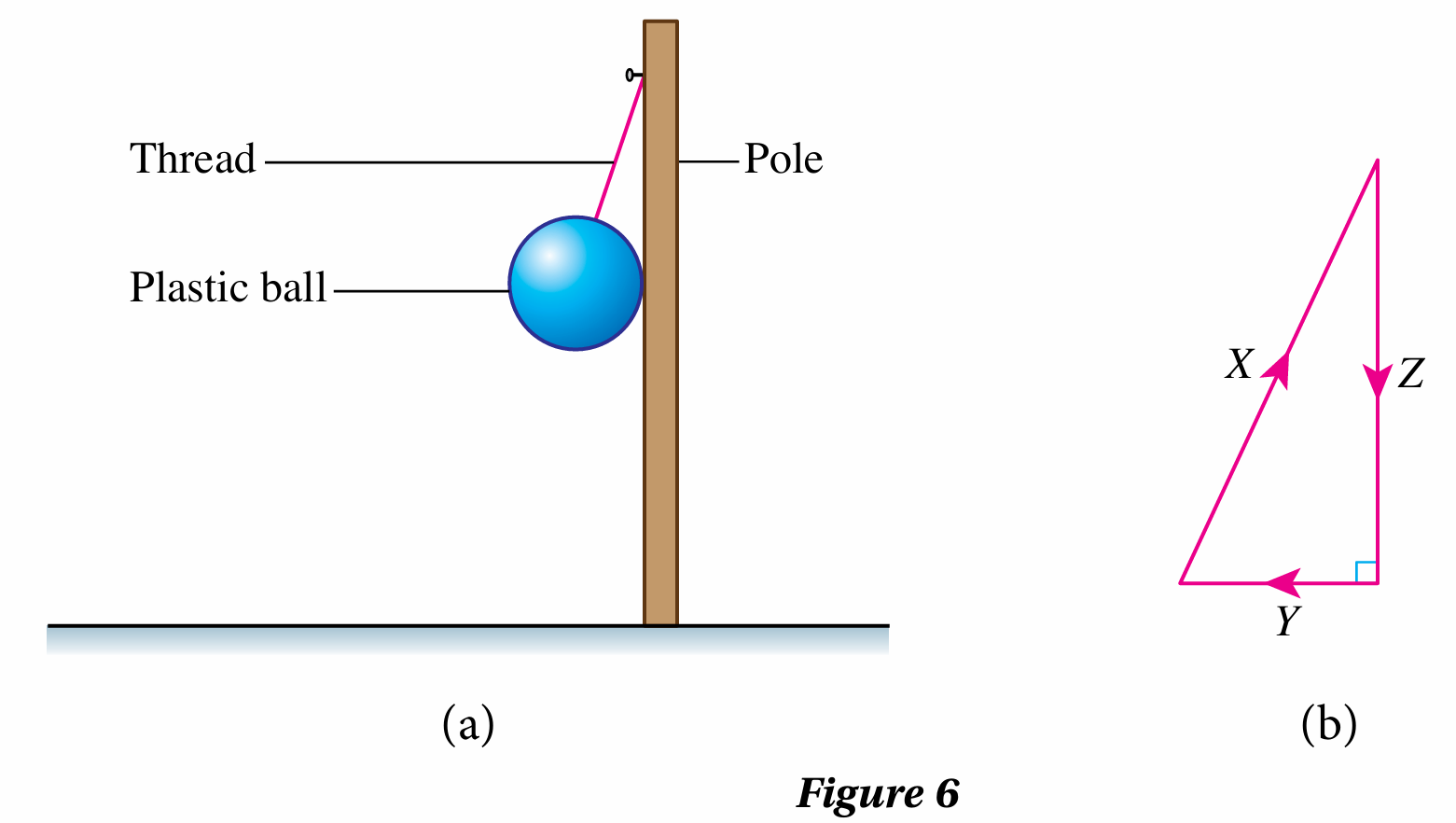
Figure 6(a) shows a plastic ball hanging from a pole. Figure 6(b) is the triangle of forces for forces X, Y and Z acting on the ball.
On Figure 6(a), sketch a free body diagram of the plastic ball.
Answer:
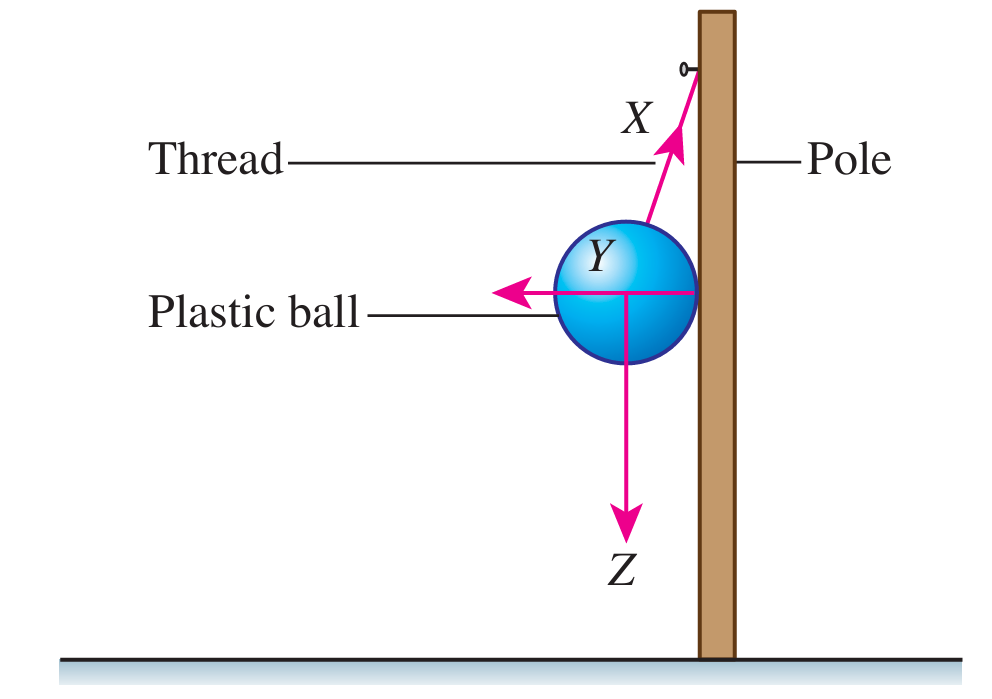
Figure 6(a) shows a plastic ball hanging from a pole. Figure 6(b) is the triangle of forces for forces X, Y and Z acting on the ball.
On Figure 6(a), sketch a free body diagram of the plastic ball.

Answer:

Question 9:
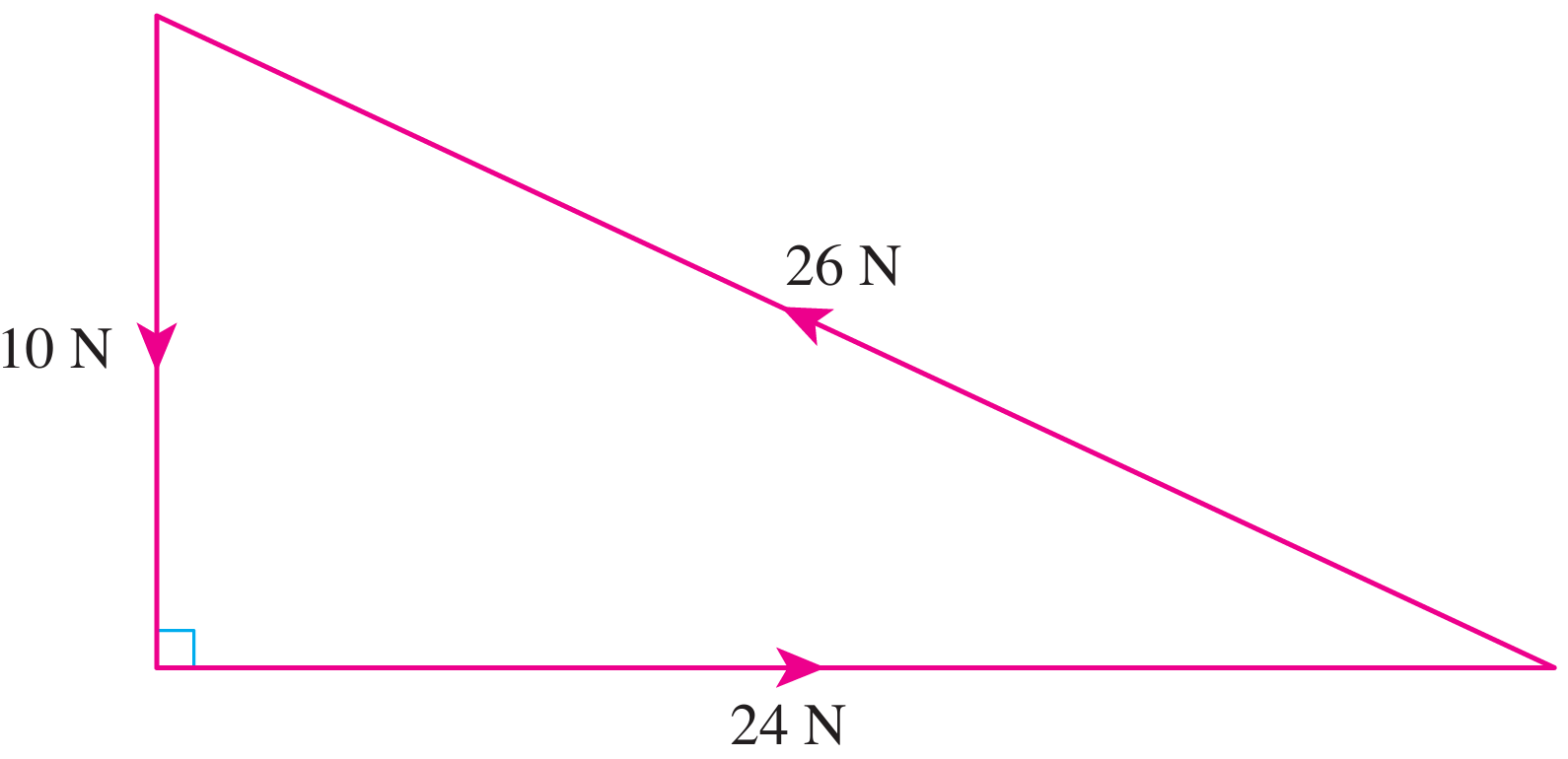
Three coplanar forces, 10 N, 24 N and 26 N act on an object. Draw a triangle of forces for the three forces if the object is in equilibrium.
Answer:
Since the object is stationary, the three coplanar forces 10 N, 24 N, 26 N are in equilibrium.
$$ \begin{aligned} &\begin{aligned} 10^2+24^2 & =676 \\ 26^2 & =676 \end{aligned}\\ &\text { That is, } 10^2+24^2=26^2 \end{aligned} $$
The three forces drawn in sequence form a right-angled triangle.
Three coplanar forces, 10 N, 24 N and 26 N act on an object. Draw a triangle of forces for the three forces if the object is in equilibrium.
Answer:
Since the object is stationary, the three coplanar forces 10 N, 24 N, 26 N are in equilibrium.
$$ \begin{aligned} &\begin{aligned} 10^2+24^2 & =676 \\ 26^2 & =676 \end{aligned}\\ &\text { That is, } 10^2+24^2=26^2 \end{aligned} $$
The three forces drawn in sequence form a right-angled triangle.

