Question 4:
A car of mass 1 200 kg at rest is moved by a force of 150 N. Determine the acceleration of the car and time taken for the car to reach a velocity of 1.5 m s–1.
Answer:
$$ \begin{aligned} F & =m a \\ 150 & =(1200) a \\ a & =0.125 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
$$ \begin{aligned} v & =u+a t \\ 1.5 & =0+(0.125) t \\ t & =12 \mathrm{~s} \end{aligned} $$
A car of mass 1 200 kg at rest is moved by a force of 150 N. Determine the acceleration of the car and time taken for the car to reach a velocity of 1.5 m s–1.
Answer:
$$ \begin{aligned} F & =m a \\ 150 & =(1200) a \\ a & =0.125 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
$$ \begin{aligned} v & =u+a t \\ 1.5 & =0+(0.125) t \\ t & =12 \mathrm{~s} \end{aligned} $$
Question 5:
Gravitational fi eld strength on the Moon is 6 times lower than that on Earth. If a stone weighing 2 N is carried back from the Moon to Earth, calculate the weight of the stone on Earth.
Answer:
$$ \begin{aligned} W_{\text {Moon }} & =m g_{\text {Moon }} \\ 2 & =m \times \frac{1}{6} g \\ m & =\frac{12}{g} \end{aligned} $$
$$ \begin{aligned} W_{\text {Earth }} & =m g \\ & =\frac{12}{g} \times g \\ & =12 \mathrm{~N} \end{aligned} $$
Gravitational fi eld strength on the Moon is 6 times lower than that on Earth. If a stone weighing 2 N is carried back from the Moon to Earth, calculate the weight of the stone on Earth.
Answer:
$$ \begin{aligned} W_{\text {Moon }} & =m g_{\text {Moon }} \\ 2 & =m \times \frac{1}{6} g \\ m & =\frac{12}{g} \end{aligned} $$
$$ \begin{aligned} W_{\text {Earth }} & =m g \\ & =\frac{12}{g} \times g \\ & =12 \mathrm{~N} \end{aligned} $$
Question 6:
A bullet of mass 10 g is fi red from a gun of mass 2.0 kg. If the recoil velocity of the gun aft er fi ring the shot is 0.5 m s–1, calculate the velocity of the bullet.
Answer:
$$ \begin{aligned} m_1 u_1+m_2 u_2 & =m_1 v_1+m_2 v_2 \\ 0 & =m_1 v_1+m_2 v_2 \\ 0 & =\frac{10}{1000} v_1+2 \times(-0.5) \\ \frac{1}{100} v_1 & =1 \\ v_1 & =100 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
A bullet of mass 10 g is fi red from a gun of mass 2.0 kg. If the recoil velocity of the gun aft er fi ring the shot is 0.5 m s–1, calculate the velocity of the bullet.
Answer:
$$ \begin{aligned} m_1 u_1+m_2 u_2 & =m_1 v_1+m_2 v_2 \\ 0 & =m_1 v_1+m_2 v_2 \\ 0 & =\frac{10}{1000} v_1+2 \times(-0.5) \\ \frac{1}{100} v_1 & =1 \\ v_1 & =100 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
Question 7:
Photograph 1 shows a car moving along a road. Initially, the car moves at a uniform velocity of 18 m s–1 for 15 s. Then, the car accelerates at 1.5 m s–2 for 5 s. Subsequently, the car starts to decelerate to 15 m s–1 in 5 s. The car continues to move at this speed for 10 s and finally decelerates again and stops at time, t = 50 s

Based on the given information, sketch the velocity-time graph for the motion of the car.
Show the values of velocity and time in your sketch.
Answer:
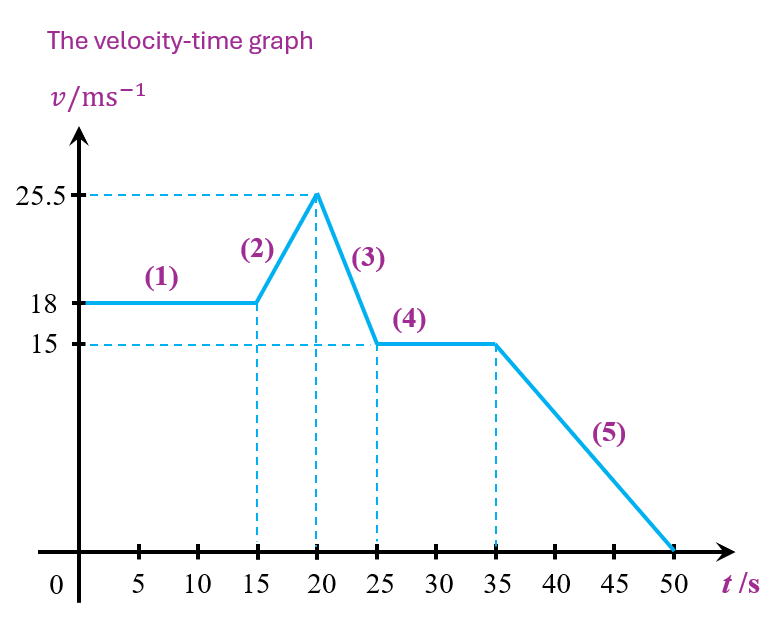
$$ \text { (1) Uniform velocity of } 18 \mathrm{~m} \mathrm{~s}^{-1} \text { for } 15 \mathrm{~s} $$
$$ \begin{aligned} &\text { (2) Car accelerates at } 1.5 \mathrm{~m} \mathrm{~s}^{-2} \text { for } 5 \mathrm{~s}\\ &\begin{aligned} v & =u+a t \\ & =18+(1.5)(5) \\ & =25.5 \mathrm{~ms}^{-1} \end{aligned} \end{aligned} $$
$$ \text { (3) The car starts to decelerate to } 15 \mathrm{~m} \mathrm{~s}^{-1} \text { in } 5 \mathrm{~s} \text {. } $$
$$ \text { (4) Uniform velocity for } 10 \mathrm{~s} $$
$$ \text { (5) Car decelerates again and stops at time } t=50 \mathrm{~s} $$
Photograph 1 shows a car moving along a road. Initially, the car moves at a uniform velocity of 18 m s–1 for 15 s. Then, the car accelerates at 1.5 m s–2 for 5 s. Subsequently, the car starts to decelerate to 15 m s–1 in 5 s. The car continues to move at this speed for 10 s and finally decelerates again and stops at time, t = 50 s

Based on the given information, sketch the velocity-time graph for the motion of the car.
Show the values of velocity and time in your sketch.
Answer:

$$ \text { (1) Uniform velocity of } 18 \mathrm{~m} \mathrm{~s}^{-1} \text { for } 15 \mathrm{~s} $$
$$ \begin{aligned} &\text { (2) Car accelerates at } 1.5 \mathrm{~m} \mathrm{~s}^{-2} \text { for } 5 \mathrm{~s}\\ &\begin{aligned} v & =u+a t \\ & =18+(1.5)(5) \\ & =25.5 \mathrm{~ms}^{-1} \end{aligned} \end{aligned} $$
$$ \text { (3) The car starts to decelerate to } 15 \mathrm{~m} \mathrm{~s}^{-1} \text { in } 5 \mathrm{~s} \text {. } $$
$$ \text { (4) Uniform velocity for } 10 \mathrm{~s} $$
$$ \text { (5) Car decelerates again and stops at time } t=50 \mathrm{~s} $$
