Question 8:
A rubber ball is released from a height, H. The ball drops vertically downwards and upon hitting the floor, bounces back a height, h (h < H). If the velocity of downward motion is negative, sketch the velocity-time graph for the motion of the rubber ball.
Answer:
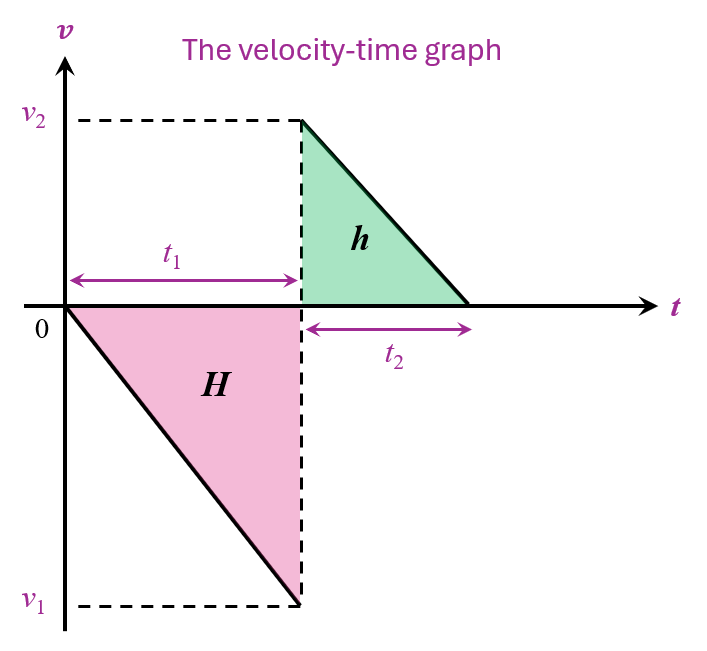
For velocity-time graph:
Gradient of the graph = acceleration
Area under the graph = displacement
v2 < v1
t2 < t1
because h < H
A rubber ball is released from a height, H. The ball drops vertically downwards and upon hitting the floor, bounces back a height, h (h < H). If the velocity of downward motion is negative, sketch the velocity-time graph for the motion of the rubber ball.
Answer:

For velocity-time graph:
Gradient of the graph = acceleration
Area under the graph = displacement
v2 < v1
t2 < t1
because h < H
Question 9:
A car at rest starts to move when a bus moves at a uniform velocity of 15 m s–1 passes by its side. The car reaches a velocity of 20 m s–1 in 10 seconds and continues to move at a constant velocity in the same direction with the bus. The graph in Figure 1 shows the motion of the car and the bus along a straight road.
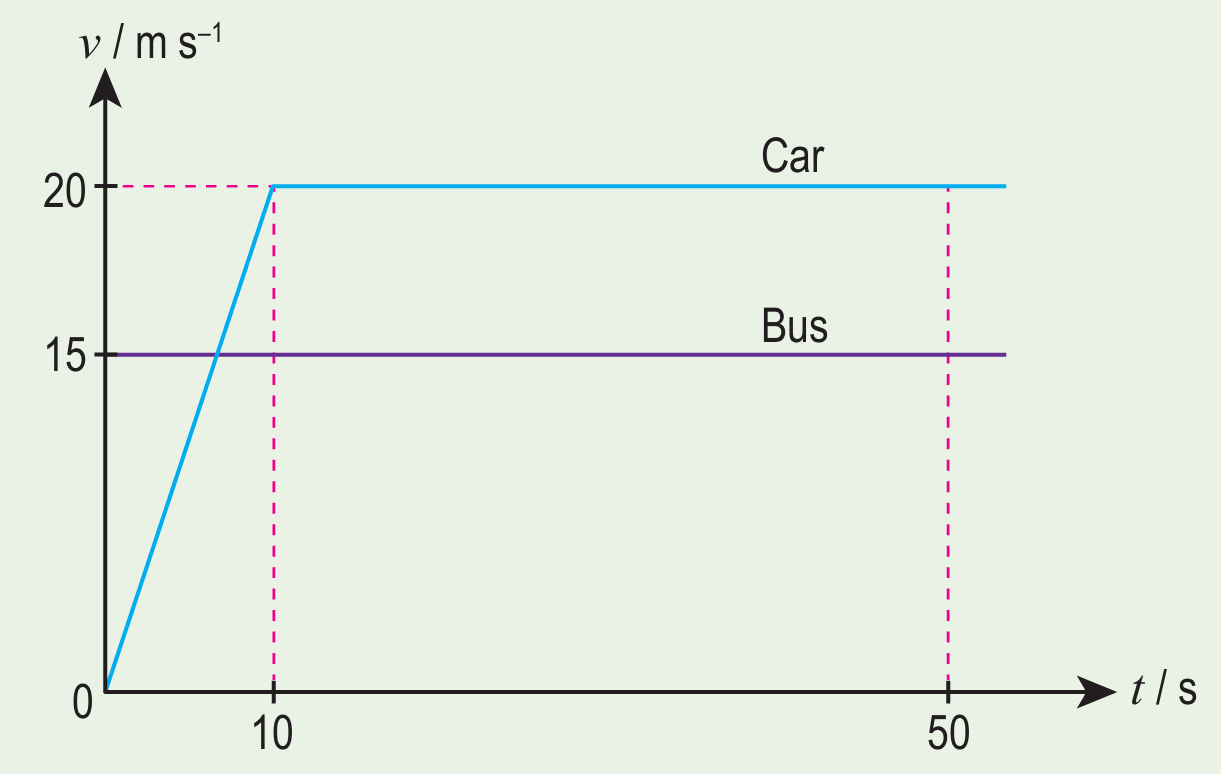
(a) Calculate the time taken for the car to reach the same speed as the bus.
(b) What is the displacement of the car when it reaches the speed of the bus?
(c) Calculate the distance travelled by the car and bus at time, t = 50 s.
(d) At time, t = 50 s, is the car in front of the bus?
Answer:
(a)
$$ \begin{aligned} & \text { Acceleration }=\text { gradient of graph } \\ & \text { Acceleration of car, } \begin{aligned} a & =\frac{20}{10} \\ & =2 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} \end{aligned} $$
To find the time taken for the car to achieve the speed of the bus 15 ms-1, use the equation
$$ \begin{aligned} v & =u+a t \\ 15 & =0+2 t \\ t & =7.5 \mathrm{~s} \end{aligned} $$
(b)
The displacement of the car when it reaches the speed of the bus. Acceleration of car, 15 ms-2 at time t = 7.5 s
$$ \begin{aligned} s & =u t+\frac{1}{2} a t^2 \\ & =0+\frac{1}{2}(2)(7.5)^2 \\ & =56.25 \mathrm{~m} \end{aligned} $$
(c)
To find the distance travelled in time t = 50 s ⇒ Distance = area below the graph
$$ \begin{aligned} \text { For car, distance travelled } & =\text { Area of trapezium } \\ & =\frac{1}{2}(40+50) 20 \\ & =900 \mathrm{~m} \\ \text { For bus, distance travelled } & =\text { Area of rectangle } \\ & =50 \times 15 \\ & =750 \mathrm{~m} \end{aligned} $$
(d)
The distance travelled by the car is longer than the distance travelled by the bus therefore the car is in front of the bus.
$$ \begin{aligned} &\text { Distance separating the car from the bus }\\ &\begin{aligned} & =900-750 \\ & =150 \mathrm{~m} \end{aligned} \end{aligned} $$
A car at rest starts to move when a bus moves at a uniform velocity of 15 m s–1 passes by its side. The car reaches a velocity of 20 m s–1 in 10 seconds and continues to move at a constant velocity in the same direction with the bus. The graph in Figure 1 shows the motion of the car and the bus along a straight road.

(a) Calculate the time taken for the car to reach the same speed as the bus.
(b) What is the displacement of the car when it reaches the speed of the bus?
(c) Calculate the distance travelled by the car and bus at time, t = 50 s.
(d) At time, t = 50 s, is the car in front of the bus?
Answer:

(a)
$$ \begin{aligned} & \text { Acceleration }=\text { gradient of graph } \\ & \text { Acceleration of car, } \begin{aligned} a & =\frac{20}{10} \\ & =2 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} \end{aligned} $$
To find the time taken for the car to achieve the speed of the bus 15 ms-1, use the equation
$$ \begin{aligned} v & =u+a t \\ 15 & =0+2 t \\ t & =7.5 \mathrm{~s} \end{aligned} $$
(b)
The displacement of the car when it reaches the speed of the bus. Acceleration of car, 15 ms-2 at time t = 7.5 s
$$ \begin{aligned} s & =u t+\frac{1}{2} a t^2 \\ & =0+\frac{1}{2}(2)(7.5)^2 \\ & =56.25 \mathrm{~m} \end{aligned} $$
(c)
To find the distance travelled in time t = 50 s ⇒ Distance = area below the graph
$$ \begin{aligned} \text { For car, distance travelled } & =\text { Area of trapezium } \\ & =\frac{1}{2}(40+50) 20 \\ & =900 \mathrm{~m} \\ \text { For bus, distance travelled } & =\text { Area of rectangle } \\ & =50 \times 15 \\ & =750 \mathrm{~m} \end{aligned} $$
(d)
The distance travelled by the car is longer than the distance travelled by the bus therefore the car is in front of the bus.
$$ \begin{aligned} &\text { Distance separating the car from the bus }\\ &\begin{aligned} & =900-750 \\ & =150 \mathrm{~m} \end{aligned} \end{aligned} $$
Question 10:
Photograph 2 shows the launching of a spacecraft using a rocket at a launch pad.

(a) Explain how the release of hot gases through the rocket’s exhaust enables the rocket to accelerate upwards.
(b) How can the acceleration of this rocket be increased?
Answer:
(a)
Before the launch, the rocket carrying a spacecraft is at rest at the launch pad with zero momentum.
During the launch, a large amount of fast moving hot gases is released through the exhaust. This creates/cause high downward momentum.
According to the principle of conservation of momentum, an equally high but opposite momentum is produced.
Hence an upthrust gives an acceleration to the rocket.
(b) Acceleration of the rocket can be increased by reducing the mass of the rocket.
Photograph 2 shows the launching of a spacecraft using a rocket at a launch pad.

(a) Explain how the release of hot gases through the rocket’s exhaust enables the rocket to accelerate upwards.
(b) How can the acceleration of this rocket be increased?
Answer:
(a)
Before the launch, the rocket carrying a spacecraft is at rest at the launch pad with zero momentum.
During the launch, a large amount of fast moving hot gases is released through the exhaust. This creates/cause high downward momentum.
According to the principle of conservation of momentum, an equally high but opposite momentum is produced.
Hence an upthrust gives an acceleration to the rocket.
(b) Acceleration of the rocket can be increased by reducing the mass of the rocket.
