Question 4:
A weather satellite orbits the Earth at a height of 560 km. What is the value of gravitational acceleration at the position of the satellite?
[G = 6.67 × 10–11 N m2 kg–2, mass of the Earth = 5.97 × 1024 kg, radius of the Earth = 6.37 × 106 m]
Answer:
$$ \begin{aligned} h & =560 \mathrm{~km}=5.60 \times 10^5 \mathrm{~m} \\ G & =6.67 \times 10^{-11} \mathrm{Nm}^2 \mathrm{~kg}^{-2} \\ M_E & =5.97 \times 10^{24} \mathrm{~kg} \\ r & =6.37 \times 10^6 \mathrm{~m} \\ g & =? \end{aligned} $$
$$ \begin{aligned} g & =\frac{G M}{r^2}=\frac{G M}{(R+h)^2} \\ r & =R+h \\ & =5.60 \times 10^5+6.37 \times 10^6 \\ & =6.93 \times 10^6 \mathrm{~m} \\ g & =\frac{\left(6.67 \times 10^{-11}\right) \times\left(5.97 \times 10^{24}\right)}{\left(6.93 \times 10^6\right)^2} \\ g & =8.29 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
A weather satellite orbits the Earth at a height of 560 km. What is the value of gravitational acceleration at the position of the satellite?
[G = 6.67 × 10–11 N m2 kg–2, mass of the Earth = 5.97 × 1024 kg, radius of the Earth = 6.37 × 106 m]
Answer:
$$ \begin{aligned} h & =560 \mathrm{~km}=5.60 \times 10^5 \mathrm{~m} \\ G & =6.67 \times 10^{-11} \mathrm{Nm}^2 \mathrm{~kg}^{-2} \\ M_E & =5.97 \times 10^{24} \mathrm{~kg} \\ r & =6.37 \times 10^6 \mathrm{~m} \\ g & =? \end{aligned} $$
$$ \begin{aligned} g & =\frac{G M}{r^2}=\frac{G M}{(R+h)^2} \\ r & =R+h \\ & =5.60 \times 10^5+6.37 \times 10^6 \\ & =6.93 \times 10^6 \mathrm{~m} \\ g & =\frac{\left(6.67 \times 10^{-11}\right) \times\left(5.97 \times 10^{24}\right)}{\left(6.93 \times 10^6\right)^2} \\ g & =8.29 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
Question 5:
A man-made satellite of mass 400 kg orbits the Earth with a radius of 8.2 × 106 m. Linear speed of the satellite is 6.96 × 103 m s–1. What is the centripetal force acting on the satellite?
Answer:
$$ \begin{aligned} m & =400 \mathrm{~kg} \\ r & =8.2 \times 10^6 \mathrm{~m} \\ v & =6.96 \times 10^3 \mathrm{~m} \mathrm{~s}^{-1} \\ F & =? \end{aligned} $$
$$ \begin{aligned} & F=\frac{m v^2}{r} \\ & F=\frac{(400) \times\left(6.96 \times 10^3\right)^2}{\left(8.2 \times 10^6\right)} \\ & F=2363 \mathrm{~N} \end{aligned} $$
A man-made satellite of mass 400 kg orbits the Earth with a radius of 8.2 × 106 m. Linear speed of the satellite is 6.96 × 103 m s–1. What is the centripetal force acting on the satellite?
Answer:
$$ \begin{aligned} m & =400 \mathrm{~kg} \\ r & =8.2 \times 10^6 \mathrm{~m} \\ v & =6.96 \times 10^3 \mathrm{~m} \mathrm{~s}^{-1} \\ F & =? \end{aligned} $$
$$ \begin{aligned} & F=\frac{m v^2}{r} \\ & F=\frac{(400) \times\left(6.96 \times 10^3\right)^2}{\left(8.2 \times 10^6\right)} \\ & F=2363 \mathrm{~N} \end{aligned} $$
Question 6:
Figure 3.23 shows Mercury orbiting the Sun with a radius of 5.79 × 1010 m and a period of revolution of 7.57 × 106 s. Calculate the mass of the Sun.
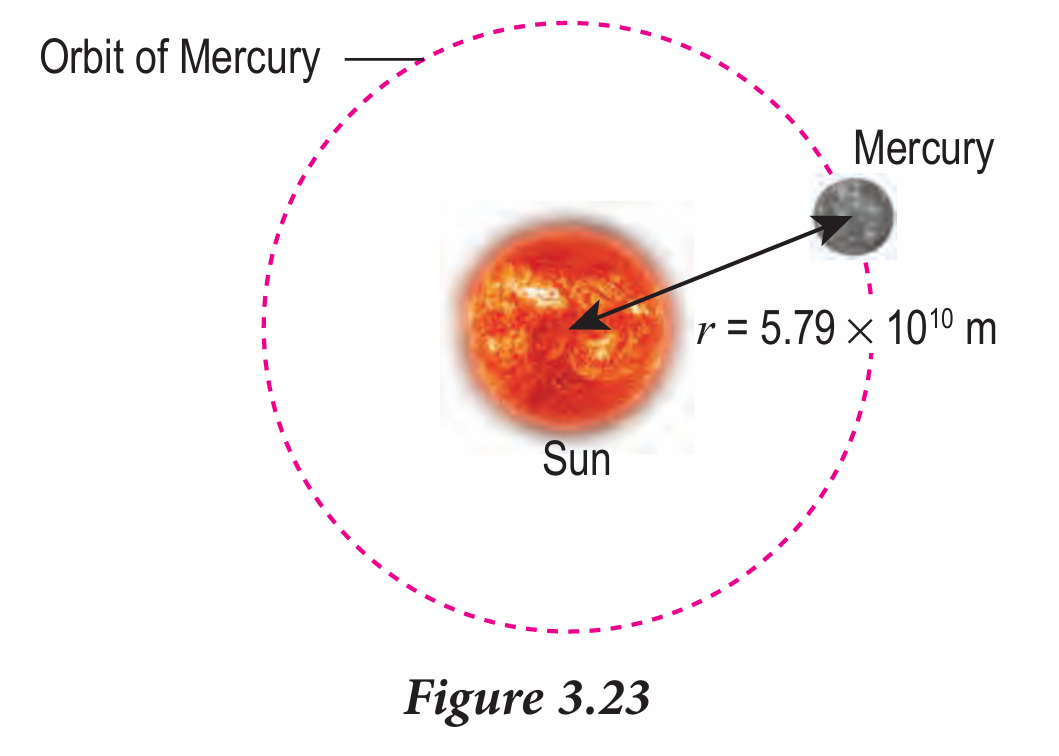
Answer:
$$ \begin{aligned} r & =5.79 \times 10^{10} \mathrm{~m} \\ T & =7.57 \times 10^6 \mathrm{~s} \\ G & =6.67 \times 10^{-11} \mathrm{Nm}^2 \mathrm{~kg}^{-2} \\ M_S & =? \end{aligned} $$
$$ \begin{aligned} M & =\frac{4 \pi^2 r^3}{G T^2} \\ M_S & =\frac{4 \pi^2\left(5.79 \times 10^{10}\right)^3}{\left(6.67 \times 10^{-11}\right) \times\left(7.57 \times 10^6\right)^2} \\ M_S & =2.005 \times 10^{30} \mathrm{~kg} \end{aligned} $$
Figure 3.23 shows Mercury orbiting the Sun with a radius of 5.79 × 1010 m and a period of revolution of 7.57 × 106 s. Calculate the mass of the Sun.

Answer:
$$ \begin{aligned} r & =5.79 \times 10^{10} \mathrm{~m} \\ T & =7.57 \times 10^6 \mathrm{~s} \\ G & =6.67 \times 10^{-11} \mathrm{Nm}^2 \mathrm{~kg}^{-2} \\ M_S & =? \end{aligned} $$
$$ \begin{aligned} M & =\frac{4 \pi^2 r^3}{G T^2} \\ M_S & =\frac{4 \pi^2\left(5.79 \times 10^{10}\right)^3}{\left(6.67 \times 10^{-11}\right) \times\left(7.57 \times 10^6\right)^2} \\ M_S & =2.005 \times 10^{30} \mathrm{~kg} \end{aligned} $$
