Question 1:
State Kepler’s first law.
Answer:
Kepler’s first law states that all planets move in elliptical orbits with the Sun at one focus.
State Kepler’s first law.
Answer:
Kepler’s first law states that all planets move in elliptical orbits with the Sun at one focus.
Question 2:
(a) State Kepler’s second law.
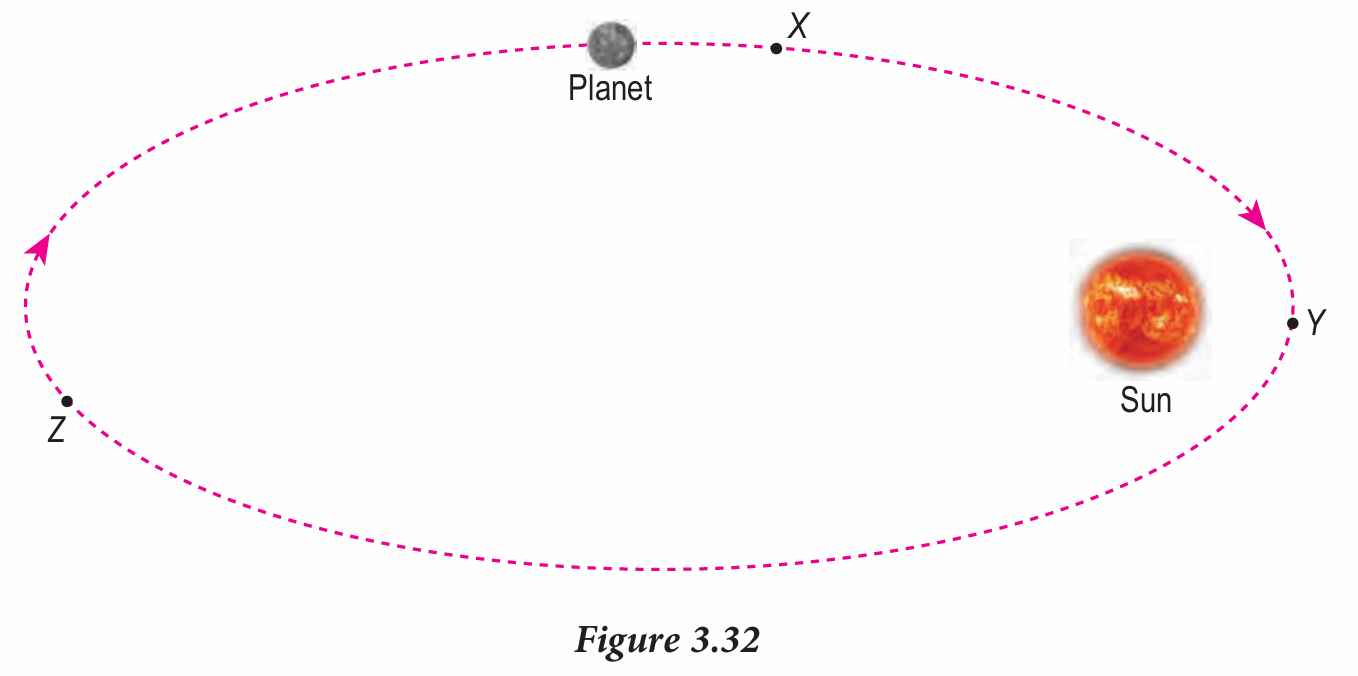
(b) Figure 3.32 shows the orbit of a planet around the Sun. Compare the linear speed of the planet at positions X, Y and Z.
Answer:
(a) Kepler’s second law states that a line that connects a planet to the Sun sweeps out equal areas in equal times.
(b)
(a) State Kepler’s second law.
(b) Figure 3.32 shows the orbit of a planet around the Sun. Compare the linear speed of the planet at positions X, Y and Z.

Answer:
(a) Kepler’s second law states that a line that connects a planet to the Sun sweeps out equal areas in equal times.
(b)

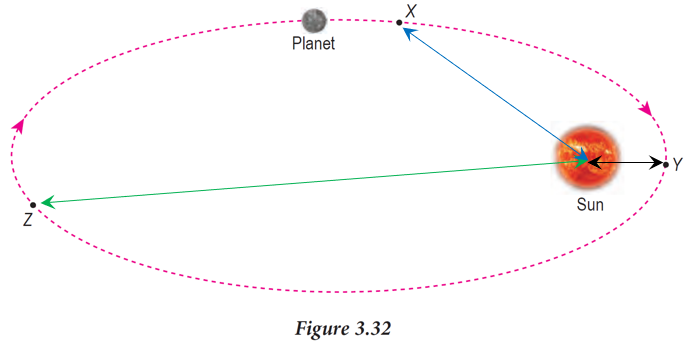
The further the distance from the sun, the lower the linear speed of the planet.
Thus, the linear speed of the planet at positions X, Y and Z is vY > vX > vZ.Question 3:
(a) State Kepler’s third law.
(b) At what height should a satellite be if the satellite is required to orbit the Earth in a period of 24 hours?
[Orbital period of the Moon = 27.3 days, radius of orbit of the Moon = 3.83 × 108 m]
Answer:
(a) Kepler’s third law states that the square of the orbital period of any planet is directly proportional to the cube of the radius of its orbit.
(b)
$$ \begin{aligned} & \text { Radius of earth, } r_E=6.37 \times 10^6 \mathrm{~m} \\ & \text { Radius of moon, } r_m=3.83 \times 10^8 \mathrm{~m} \\ & \text { Period of moon, } T_m=27.3 \text { hari } \\ & \text { Period of satellite, } T_s=1 \text { day } \\ & \text { Radius of satellite, } r_s=\left(6.37 \times 10^6\right)+h \\ & \frac{T_m^2}{T_s^2}=\frac{r_m^3}{r_s^3} \\ & \frac{27.3^2}{1^2}=\frac{\left(3.83 \times 10^8\right)^3}{\left(r_E+h\right)^3} \\ & \left(r_E+h\right)^3=\frac{\left(3.83 \times 10^8\right)^3 \times 1}{(27.3)^2} \\ & r_E+h=\sqrt[3]{\frac{\left(3.83 \times 10^8\right)^3 \times 1}{(27.3)^2}} \\ & r_E+h=4.22 \times 10^7 \mathrm{~m} \\ & h=4.22 \times 10^7 \mathrm{~m}-6.37 \times 10^6 \mathrm{~m} \\ & h=3.58 \times 10^7 \mathrm{~m} \\ & \end{aligned} $$
(a) State Kepler’s third law.
(b) At what height should a satellite be if the satellite is required to orbit the Earth in a period of 24 hours?
[Orbital period of the Moon = 27.3 days, radius of orbit of the Moon = 3.83 × 108 m]
Answer:
(a) Kepler’s third law states that the square of the orbital period of any planet is directly proportional to the cube of the radius of its orbit.
(b)
$$ \begin{aligned} & \text { Radius of earth, } r_E=6.37 \times 10^6 \mathrm{~m} \\ & \text { Radius of moon, } r_m=3.83 \times 10^8 \mathrm{~m} \\ & \text { Period of moon, } T_m=27.3 \text { hari } \\ & \text { Period of satellite, } T_s=1 \text { day } \\ & \text { Radius of satellite, } r_s=\left(6.37 \times 10^6\right)+h \\ & \frac{T_m^2}{T_s^2}=\frac{r_m^3}{r_s^3} \\ & \frac{27.3^2}{1^2}=\frac{\left(3.83 \times 10^8\right)^3}{\left(r_E+h\right)^3} \\ & \left(r_E+h\right)^3=\frac{\left(3.83 \times 10^8\right)^3 \times 1}{(27.3)^2} \\ & r_E+h=\sqrt[3]{\frac{\left(3.83 \times 10^8\right)^3 \times 1}{(27.3)^2}} \\ & r_E+h=4.22 \times 10^7 \mathrm{~m} \\ & h=4.22 \times 10^7 \mathrm{~m}-6.37 \times 10^6 \mathrm{~m} \\ & h=3.58 \times 10^7 \mathrm{~m} \\ & \end{aligned} $$
