Question 1:
Figure 1 shows planet Mars orbits the Sun in a circular motion with orbital period, T.
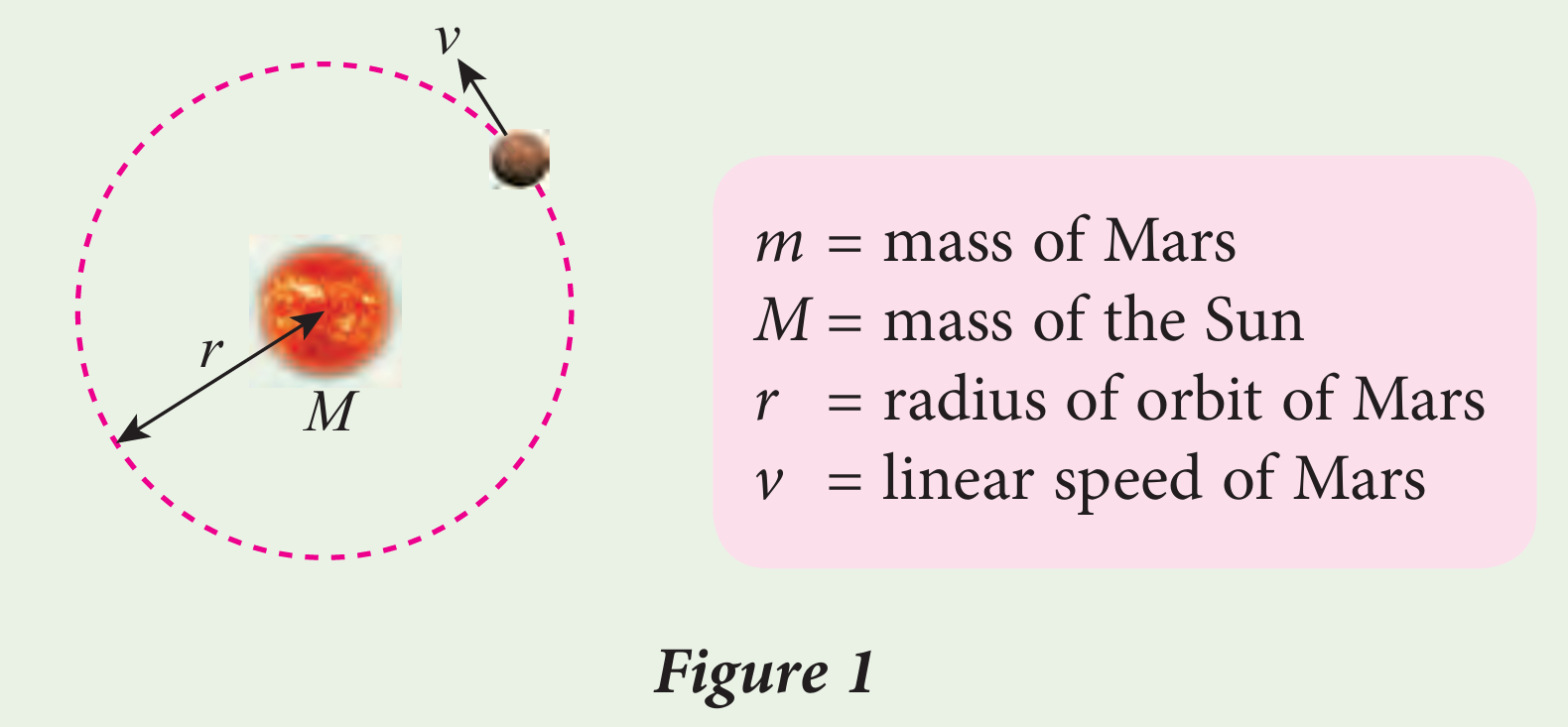
(a) For planet Mars, write the formula for:
(i) gravitational force in terms of m, M and r
(ii) centripetal force in terms of m, v and r
(iii) linear speed in terms of r and T
(b) Derive an expression for the mass of the Sun in terms of r and T by using the three formulae in (a).
(c) Radius of orbit of Mars is r = 2.28 × 1011 m and its orbital period is T = 687 days.
Calculate the mass of the Sun.
Answer:
(a)(i)
$$ F=\frac{G M m}{r^2} $$
(a)(ii)
$$ F=\frac{m v^2}{r} $$
(a)(iii)
$$ v=\frac{2 \pi r}{T} $$
(b)
Gravitational force acts as centripetal force $$ \begin{aligned} \frac{G M m}{r^2} & =\frac{m v^2}{r} \\ \text { Cancel } m, \quad \frac{G M}{r^2} & =\frac{v^2}{r} \end{aligned} $$
Substitute $$ \begin{aligned} v=\frac{2 \pi r}{T}, \quad \frac{G M}{r^2} & =\frac{1}{r}\left(\frac{2 \pi r}{T}\right)^2 \\ \frac{G M}{r^2} & =\frac{1}{r}\left(\frac{4 \pi^2 r^2}{T^2}\right) \\ M & =\frac{1}{r}\left(\frac{4 \pi^2 r^2}{T^2}\right) \frac{r^2}{G} \\ M & =\frac{4 \pi^2 r^3}{G T^2} \end{aligned} $$
(c)
$$ \begin{aligned} & 1 \text { day }=24 \text { hours, } 1 \text { hour }=3600 \mathrm{~s} \\ & T=687 \text { days } \\ & =(687 \times 24 \times 3600) s \\ & M=\frac{4 \pi^2 r^3}{G T^2} \\ & M=\frac{4 \pi^2\left(2.28 \times 10^{11}\right)^3}{\left(6.67 \times 10^{-11}\right)(687 \times 24 \times 3600)^2} \\ & =1.99 \times 10^{30} \mathrm{~kg} \\ & \end{aligned} $$
Figure 1 shows planet Mars orbits the Sun in a circular motion with orbital period, T.

(a) For planet Mars, write the formula for:
(i) gravitational force in terms of m, M and r
(ii) centripetal force in terms of m, v and r
(iii) linear speed in terms of r and T
(b) Derive an expression for the mass of the Sun in terms of r and T by using the three formulae in (a).
(c) Radius of orbit of Mars is r = 2.28 × 1011 m and its orbital period is T = 687 days.
Calculate the mass of the Sun.
Answer:
(a)(i)
$$ F=\frac{G M m}{r^2} $$
(a)(ii)
$$ F=\frac{m v^2}{r} $$
(a)(iii)
$$ v=\frac{2 \pi r}{T} $$
(b)
Gravitational force acts as centripetal force $$ \begin{aligned} \frac{G M m}{r^2} & =\frac{m v^2}{r} \\ \text { Cancel } m, \quad \frac{G M}{r^2} & =\frac{v^2}{r} \end{aligned} $$
Substitute $$ \begin{aligned} v=\frac{2 \pi r}{T}, \quad \frac{G M}{r^2} & =\frac{1}{r}\left(\frac{2 \pi r}{T}\right)^2 \\ \frac{G M}{r^2} & =\frac{1}{r}\left(\frac{4 \pi^2 r^2}{T^2}\right) \\ M & =\frac{1}{r}\left(\frac{4 \pi^2 r^2}{T^2}\right) \frac{r^2}{G} \\ M & =\frac{4 \pi^2 r^3}{G T^2} \end{aligned} $$
(c)
$$ \begin{aligned} & 1 \text { day }=24 \text { hours, } 1 \text { hour }=3600 \mathrm{~s} \\ & T=687 \text { days } \\ & =(687 \times 24 \times 3600) s \\ & M=\frac{4 \pi^2 r^3}{G T^2} \\ & M=\frac{4 \pi^2\left(2.28 \times 10^{11}\right)^3}{\left(6.67 \times 10^{-11}\right)(687 \times 24 \times 3600)^2} \\ & =1.99 \times 10^{30} \mathrm{~kg} \\ & \end{aligned} $$
Question 2:
A satellite orbits the Earth with radius, r and orbital period, T.
(a) Write down the linear speed of the satellite in terms of r and T.
(b) Use other suitable formulae to establish the formula for linear speed of the satellite in terms of r and M. M is the mass of the Earth.
(c) Why does the linear speed of a satellite orbiting the Earth not depend on the mass of the satellite?
Answer:
(a)$$ v=\frac{S}{t}=\frac{2 \pi r}{T} $$
(b)
Gravitational force between satellite and the Earth, $$ \begin{aligned} F=\frac{G M m}{r^2}, \quad M & =\text { mass of the Earth } \\ \text { Centripetal force } & =\text { Gravitational force } \\ \frac{m v^2}{r} & =\frac{G M m}{r^2} \end{aligned} $$
(c)
Satellites fall freely around the Earth with a central acceleration equal to the acceleration of gravity. The acceleration of gravity does not depend on the mass of the object.
A satellite orbits the Earth with radius, r and orbital period, T.
(a) Write down the linear speed of the satellite in terms of r and T.
(b) Use other suitable formulae to establish the formula for linear speed of the satellite in terms of r and M. M is the mass of the Earth.
(c) Why does the linear speed of a satellite orbiting the Earth not depend on the mass of the satellite?
Answer:
(a)$$ v=\frac{S}{t}=\frac{2 \pi r}{T} $$
(b)
Gravitational force between satellite and the Earth, $$ \begin{aligned} F=\frac{G M m}{r^2}, \quad M & =\text { mass of the Earth } \\ \text { Centripetal force } & =\text { Gravitational force } \\ \frac{m v^2}{r} & =\frac{G M m}{r^2} \end{aligned} $$
Cancel mass of satellite, m $$ \begin{aligned} \frac{v^2}{r} & =\frac{G M}{r^2} \\ v^2 & =\frac{G M}{r} \\ v & =\sqrt{\frac{G M}{r}} \end{aligned} $$
(c)
Satellites fall freely around the Earth with a central acceleration equal to the acceleration of gravity. The acceleration of gravity does not depend on the mass of the object.
