Question 5:
(a) What are the factors that determine the value of the gravitational acceleration?
(b) A satellite is at a distance of 4.20 × 107 m from the centre of the Earth.
What is the value of the gravitational acceleration at this position?
[Mass of the Earth = 5.97 × 1024 kg]
Answer:
(a)
– Mass of the Earth
– Distance from the centre of the Earth
(b)
$$ \begin{aligned} g & =\frac{G M m}{r^2} \\ & =\frac{\left(6.67 \times 10^{-11}\right) \times\left(5.97 \times 10^{24}\right)}{\left(4.20 \times 10^7\right)^2} \\ & =0.23 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
(a) What are the factors that determine the value of the gravitational acceleration?
(b) A satellite is at a distance of 4.20 × 107 m from the centre of the Earth.
What is the value of the gravitational acceleration at this position?
[Mass of the Earth = 5.97 × 1024 kg]
Answer:
(a)
– Mass of the Earth
– Distance from the centre of the Earth
(b)
$$ \begin{aligned} g & =\frac{G M m}{r^2} \\ & =\frac{\left(6.67 \times 10^{-11}\right) \times\left(5.97 \times 10^{24}\right)}{\left(4.20 \times 10^7\right)^2} \\ & =0.23 \mathrm{~m} \mathrm{~s}^{-2} \end{aligned} $$
Question 6:
Figure 4 shows the Earth and planet Neptune.
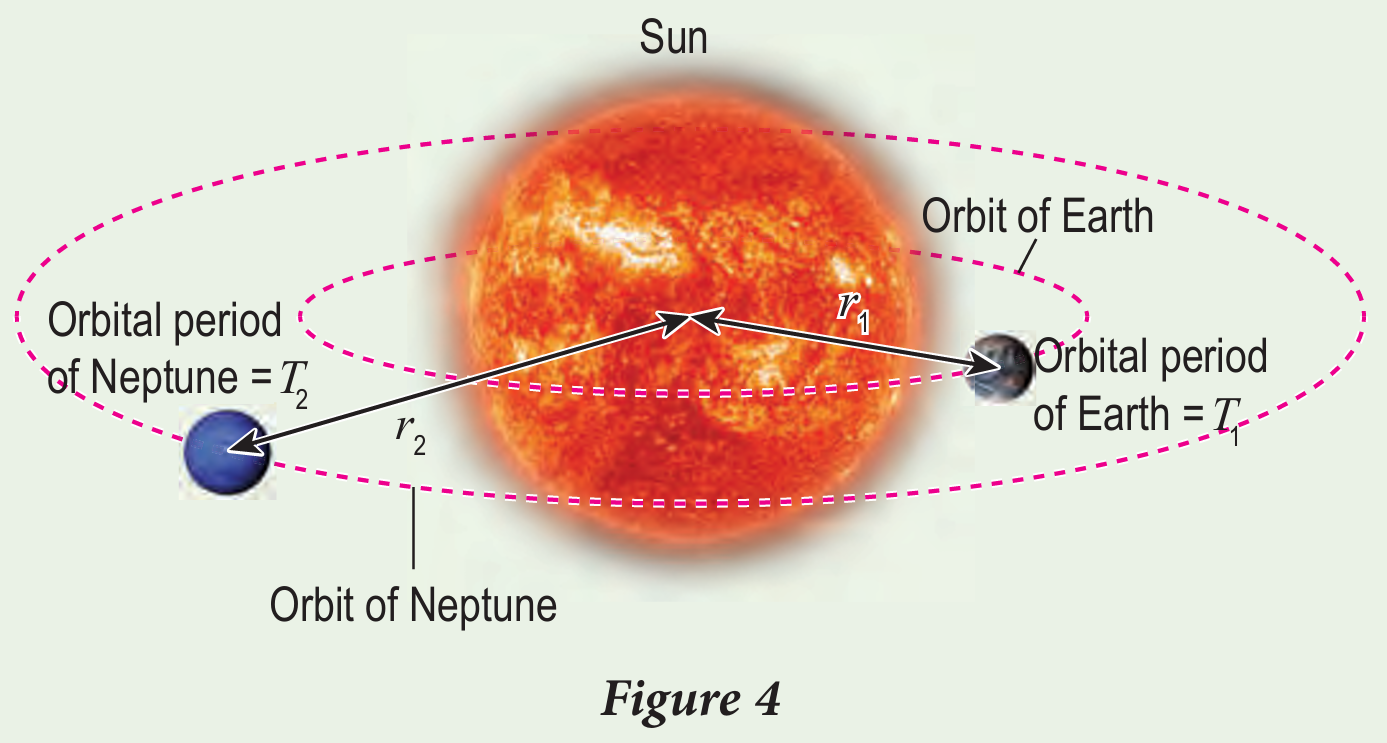
(a) Write down the relationship between orbital period and radius of orbit for the Earth and Neptune.
(b) Orbital period of the Earth is 365 days and radius of orbit of the Earth is 1.50 × 1011 m.
Calculate the radius of orbit of Neptune if its orbital period is 5.98 × 104 days.
Answer:
(a)
$$ \frac{T_1^2}{T_2^2}=\frac{r_1^3}{r_2^3} $$
(b)
Orbital period of the Earth, T1 = 365 days,
Orbital period of Neptune, T2 = 5.98 × 104 days
Orbital radius of the Earth, r1 = 1.50 × 1011 m,
Orbital radius of Neptune = r2
$$ \begin{aligned} \frac{T_1^2}{T_2^2} & =\frac{r_1^3}{r_2^3} \\ \frac{365^2}{\left(5.98 \times 10^4\right)^2} & =\frac{\left(1.50 \times 10^{11}\right)^3}{r_2^3} \\ r_2^3 & =\frac{\left(1.50 \times 10^{11}\right)^3 \times\left(5.98 \times 10^4\right)^2}{365^2} \\ r_2 & =\sqrt[3]{\frac{\left(1.50 \times 10^{11}\right)^3 \times\left(5.98 \times 10^4\right)^2}{365^2}} \\ & =4.49 \times 10^{12} \mathrm{~m} \end{aligned} $$
Figure 4 shows the Earth and planet Neptune.

(a) Write down the relationship between orbital period and radius of orbit for the Earth and Neptune.
(b) Orbital period of the Earth is 365 days and radius of orbit of the Earth is 1.50 × 1011 m.
Calculate the radius of orbit of Neptune if its orbital period is 5.98 × 104 days.
Answer:
(a)
$$ \frac{T_1^2}{T_2^2}=\frac{r_1^3}{r_2^3} $$
(b)
Orbital period of the Earth, T1 = 365 days,
Orbital period of Neptune, T2 = 5.98 × 104 days
Orbital radius of the Earth, r1 = 1.50 × 1011 m,
Orbital radius of Neptune = r2
$$ \begin{aligned} \frac{T_1^2}{T_2^2} & =\frac{r_1^3}{r_2^3} \\ \frac{365^2}{\left(5.98 \times 10^4\right)^2} & =\frac{\left(1.50 \times 10^{11}\right)^3}{r_2^3} \\ r_2^3 & =\frac{\left(1.50 \times 10^{11}\right)^3 \times\left(5.98 \times 10^4\right)^2}{365^2} \\ r_2 & =\sqrt[3]{\frac{\left(1.50 \times 10^{11}\right)^3 \times\left(5.98 \times 10^4\right)^2}{365^2}} \\ & =4.49 \times 10^{12} \mathrm{~m} \end{aligned} $$
