Question 9:
An air bubble is trapped under a leaf floating on the water surface of a lake. Th e volume of the air bubble is 3.6 cm3 when the temperature is 20°C.
(a) What is the volume of the air bubble when the water temperature rises to 38°C?
(b) State three assumptions that need to be made in your calculations in 9(a).
Answer:
(a)
(b)
– Mass of the trapped air remains unchanged.
– Pressure of the trapped air is constant.
– Trapped air and water are in thermal equilibrium. The temperatures of water and air are the same.
An air bubble is trapped under a leaf floating on the water surface of a lake. Th e volume of the air bubble is 3.6 cm3 when the temperature is 20°C.
(a) What is the volume of the air bubble when the water temperature rises to 38°C?
(b) State three assumptions that need to be made in your calculations in 9(a).
Answer:
(a)
Charles’ Law formula: $$ \begin{aligned} \frac{V_1}{T_1} & =\frac{V_2}{T_2} \\ \frac{3.6}{\left(20^{\circ} \mathrm{C}+273\right)} & =\frac{V_2}{\left(38^{\circ} \mathrm{C}+273\right)} \\ V_2 & =\frac{3.6 \times 311}{293} \\ V_2 & =3.82 \mathrm{~cm}^3 \end{aligned} $$
(b)
– Mass of the trapped air remains unchanged.
– Pressure of the trapped air is constant.
– Trapped air and water are in thermal equilibrium. The temperatures of water and air are the same.
Question 10:
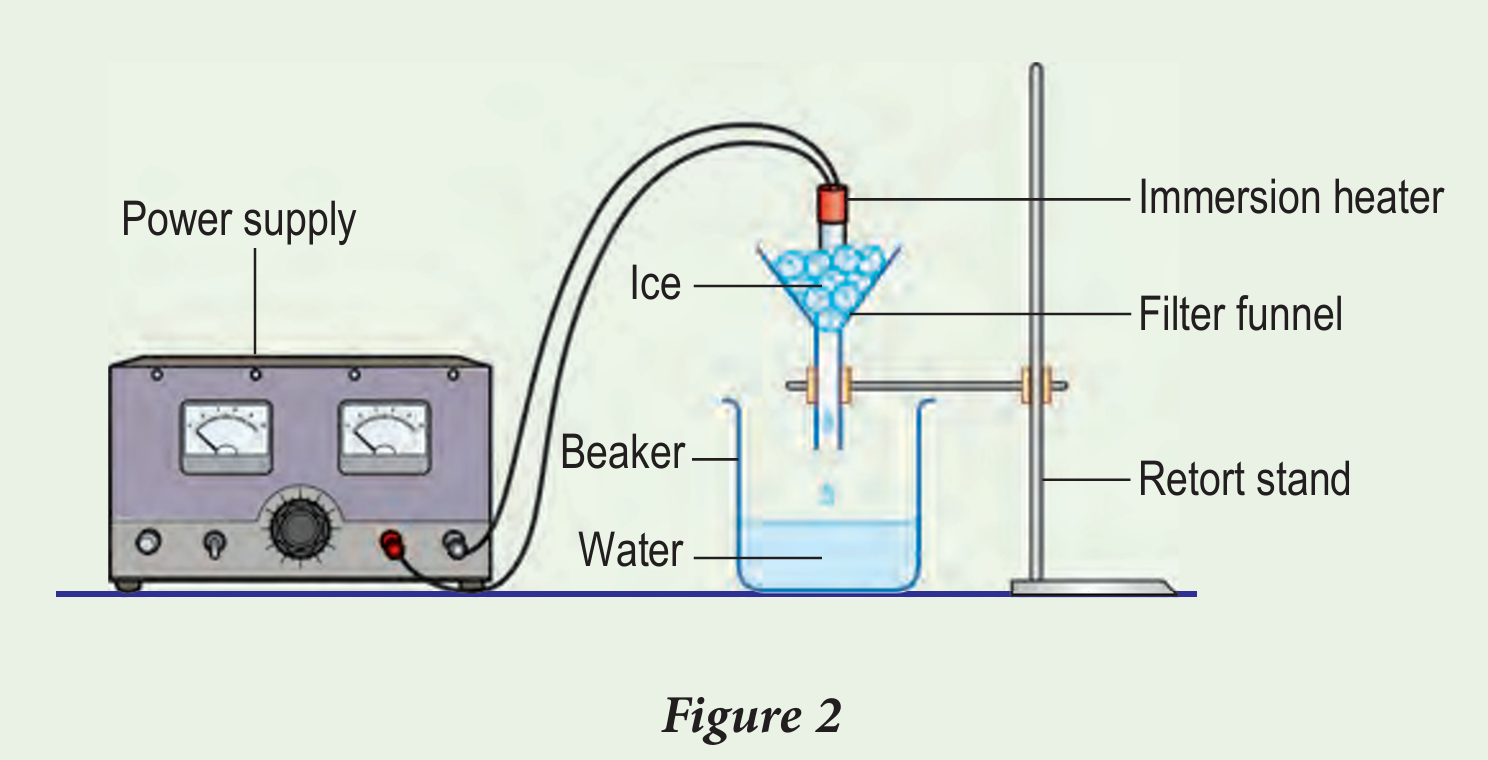
Figure 2 shows ice cubes being heated by a 500 W immersion heater for 80 seconds. The melted ice cubes are collected in a beaker.
[Specific latent heat of fusion of ice = 3.34 × 105 J kg–1]
(a) What is meant by specific latent heat of fusion?
(b) Why does the temperature remain unchanged when the ice cubes are changing into liquid?
(c) Calculate:
(i) energy absorbed by the ice cubes.
(ii) mass of melted ice cubes.
(d) What assumptions are made in your calculations in 10(c)?
Answer:
(a)
Specific latent heat of fusion, lf of a substance is the quantity of heat absorbed by 1 kg of the substance when melting or the quantity of heat released by 1 kg of the substance when freezing without any change in its temperature.
(b)
Heat absorbed does not increase the average kinetic energy of the molecules. is heat is used to weaken the bonds between the molecules of ice.
(c)(i)
\begin{aligned} Q & =P t \\ & =500 \times 80 \\ & =40000 \mathrm{~J} \end{aligned}
(c)(ii)
\begin{aligned} Q & =m l \\ 40000 & =m \times 3.34 \times 10^5 \\ m & =\frac{40000}{3.34 \times 10^5} \\ m & =0.12 \mathrm{~kg} \end{aligned}
(d)
– All the heat absorbed by the ice is supplied by the immersion heater. No heat is lost to the surroundings.
– The ice does not absorb heat from the surroundings.
Figure 2 shows ice cubes being heated by a 500 W immersion heater for 80 seconds. The melted ice cubes are collected in a beaker.
[Specific latent heat of fusion of ice = 3.34 × 105 J kg–1]

(a) What is meant by specific latent heat of fusion?
(b) Why does the temperature remain unchanged when the ice cubes are changing into liquid?
(c) Calculate:
(i) energy absorbed by the ice cubes.
(ii) mass of melted ice cubes.
(d) What assumptions are made in your calculations in 10(c)?
Answer:
(a)
Specific latent heat of fusion, lf of a substance is the quantity of heat absorbed by 1 kg of the substance when melting or the quantity of heat released by 1 kg of the substance when freezing without any change in its temperature.
(b)
Heat absorbed does not increase the average kinetic energy of the molecules. is heat is used to weaken the bonds between the molecules of ice.
(c)(i)
\begin{aligned} Q & =P t \\ & =500 \times 80 \\ & =40000 \mathrm{~J} \end{aligned}
(c)(ii)
\begin{aligned} Q & =m l \\ 40000 & =m \times 3.34 \times 10^5 \\ m & =\frac{40000}{3.34 \times 10^5} \\ m & =0.12 \mathrm{~kg} \end{aligned}
(d)
– All the heat absorbed by the ice is supplied by the immersion heater. No heat is lost to the surroundings.
– The ice does not absorb heat from the surroundings.
