Question 1:
Figure 6.16 shows the path of light which travels from medium 1 to medium 2.
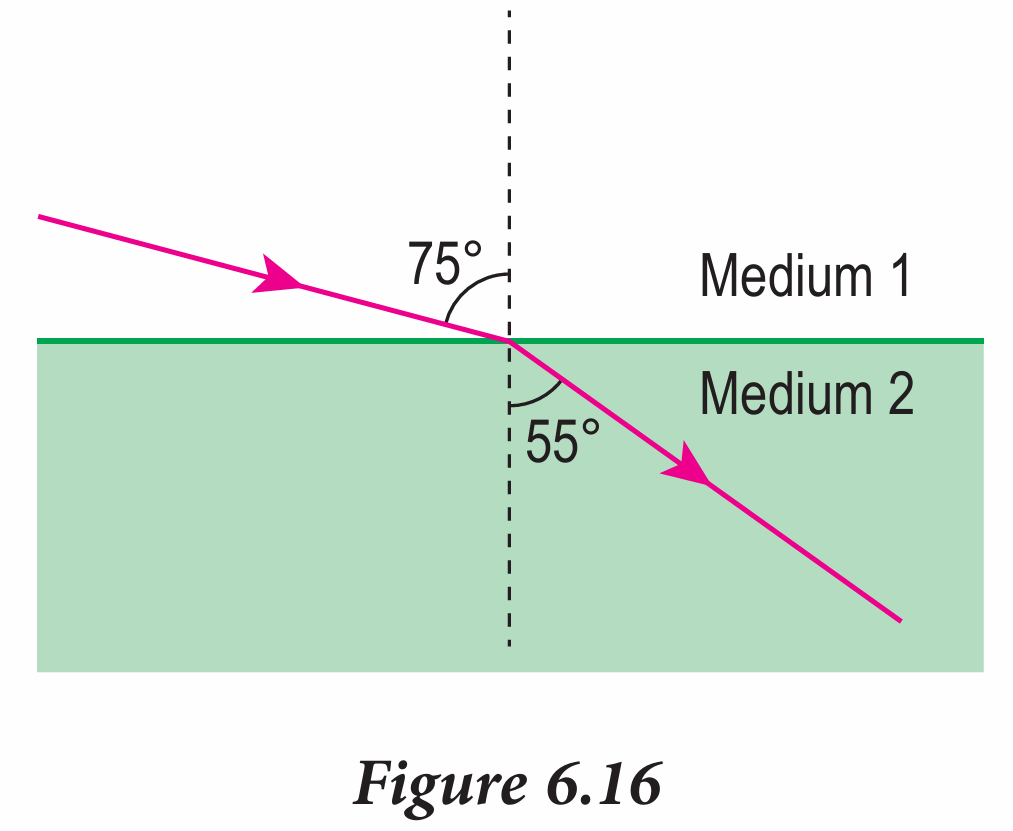
(a) Write an equation to relate the light that travels through the mediums.
(b) Determine the refractive index for medium 2 if the speed of light in medium 1 is 3.0 × 108 m s–1.
(c) What is the speed of light in medium 2?
Answer:
(a)
$$ n=\frac{\sin i}{\sin r} $$
(b)
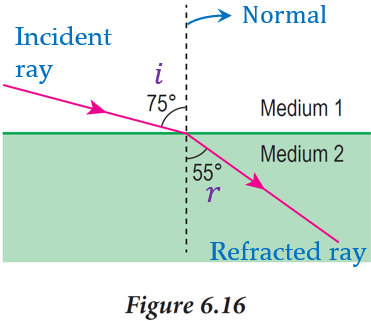
$$ \begin{aligned} & n=\frac{\sin 75^{\circ}}{\sin 55^{\circ}} \\ & n=1.18 \end{aligned} $$
(c)
$$ \text { Refractive index, } \begin{aligned} n & =\frac{\text { speed of light in vacuum }}{\text { speed of light in medium }} \\ n & =\frac{c}{v} \\ 1.18 & =\frac{3.0 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{v} \\ v & =\frac{3.0 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{1.18} \\ v & =2.54 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
Figure 6.16 shows the path of light which travels from medium 1 to medium 2.

(a) Write an equation to relate the light that travels through the mediums.
(b) Determine the refractive index for medium 2 if the speed of light in medium 1 is 3.0 × 108 m s–1.
(c) What is the speed of light in medium 2?
Answer:
(a)
$$ n=\frac{\sin i}{\sin r} $$
(b)

$$ \begin{aligned} & n=\frac{\sin 75^{\circ}}{\sin 55^{\circ}} \\ & n=1.18 \end{aligned} $$
(c)
$$ \text { Refractive index, } \begin{aligned} n & =\frac{\text { speed of light in vacuum }}{\text { speed of light in medium }} \\ n & =\frac{c}{v} \\ 1.18 & =\frac{3.0 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{v} \\ v & =\frac{3.0 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1}}{1.18} \\ v & =2.54 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
Question 2:
Figure 6.17 shows a tank filled with oil to a height of 3 m. Th e oil has a refractive index of 1.38. What is the apparent depth of the tank as seen by the observer from above the tank?
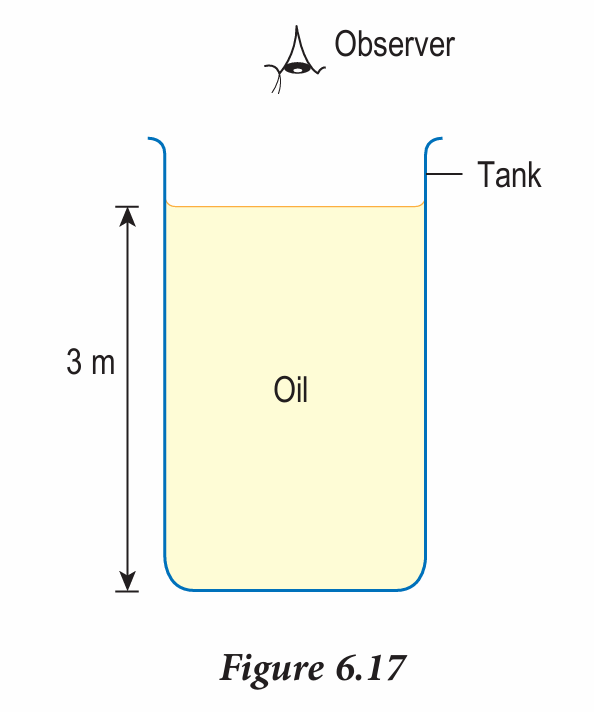
Answer:
$$ \begin{aligned} n & =\frac{\text { real depth }}{\text { apparent depth }}=\frac{H}{h} \\ 1.38 & =\frac{3 \mathrm{~m}}{h} \\ h & =\frac{3 \mathrm{~m}}{1.38} \\ & =2.17 \mathrm{~m} \end{aligned} $$
Figure 6.17 shows a tank filled with oil to a height of 3 m. Th e oil has a refractive index of 1.38. What is the apparent depth of the tank as seen by the observer from above the tank?

Answer:
$$ \begin{aligned} n & =\frac{\text { real depth }}{\text { apparent depth }}=\frac{H}{h} \\ 1.38 & =\frac{3 \mathrm{~m}}{h} \\ h & =\frac{3 \mathrm{~m}}{1.38} \\ & =2.17 \mathrm{~m} \end{aligned} $$
