Question 1:
A concave lens with a focal length of 25 cm forms a virtual image of an ant at a distance of 20 cm from the optical centre of the lens.
(a) What is the original position of the ant?
(b) Draw a ray diagram to show the formation of a virtual image of the ant.
Answer:
(a)
$$ \begin{aligned} &\begin{aligned} & f=-25 \mathrm{~cm} \text { (concave lens) } \\ & v=-20 \mathrm{~cm} \text { (virtual image) } \end{aligned}\\ &\text { Original position, } u=\text { ? } \end{aligned} $$
$$ \begin{aligned} &\text { Thin lens formula, }\\ &\begin{aligned} \frac{1}{f} & =\frac{1}{u}+\frac{1}{v} \\ \frac{1}{f}-\frac{1}{v} & =\frac{1}{u} \\ \frac{1}{-25}-\frac{1}{-20} & =\frac{1}{u} \\ \frac{4}{-100}+\frac{5}{100} & =\frac{1}{u} \\ \frac{1}{100} & =\frac{1}{u} \\ u & =100 \mathrm{~cm} \end{aligned} \end{aligned} $$
(b)
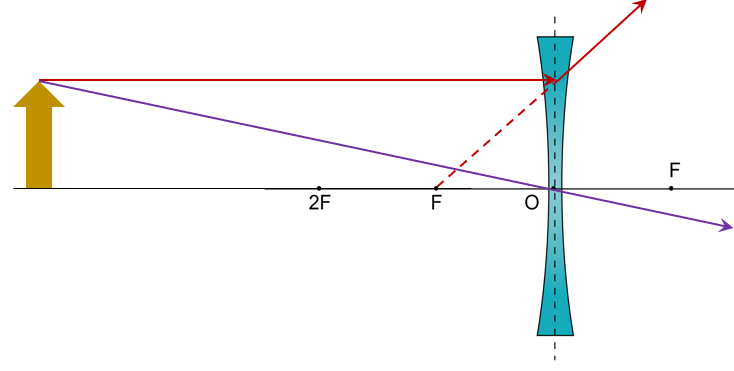
f = 25 cm, u = 100 cm, u > 2f
A concave lens with a focal length of 25 cm forms a virtual image of an ant at a distance of 20 cm from the optical centre of the lens.
(a) What is the original position of the ant?
(b) Draw a ray diagram to show the formation of a virtual image of the ant.
Answer:
(a)
$$ \begin{aligned} &\begin{aligned} & f=-25 \mathrm{~cm} \text { (concave lens) } \\ & v=-20 \mathrm{~cm} \text { (virtual image) } \end{aligned}\\ &\text { Original position, } u=\text { ? } \end{aligned} $$
$$ \begin{aligned} &\text { Thin lens formula, }\\ &\begin{aligned} \frac{1}{f} & =\frac{1}{u}+\frac{1}{v} \\ \frac{1}{f}-\frac{1}{v} & =\frac{1}{u} \\ \frac{1}{-25}-\frac{1}{-20} & =\frac{1}{u} \\ \frac{4}{-100}+\frac{5}{100} & =\frac{1}{u} \\ \frac{1}{100} & =\frac{1}{u} \\ u & =100 \mathrm{~cm} \end{aligned} \end{aligned} $$
(b)
f = 25 cm, u = 100 cm, u > 2f

Question 2:
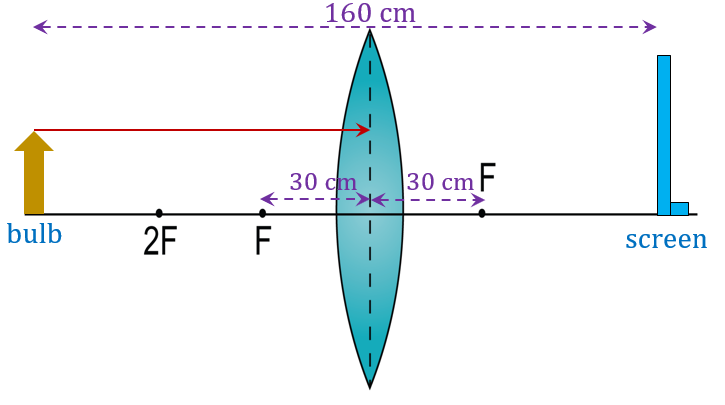
A small bulb is at a distance of 1.6 m from the screen and a thin convex lens with a focal length of 30 cm is placed between the bulb and the screen. Determine two positions of the convex lens that can produce a sharp image on the screen.
Answer:
$$ f=30 \mathrm{~cm}, \quad u=+, v=+ \text { (convex lens) } $$
$$ \begin{aligned} &\text { Thin lens formula, }\\ &\begin{aligned} \frac{1}{f} & =\frac{1}{u}+\frac{1}{v} \\ \frac{1}{f} & =\frac{u+v}{v u} \\ \frac{1}{30} & =\frac{u+v}{v u} \\ v u & =30 u+30 v \ldots(1) \end{aligned} \end{aligned} $$
$$ \begin{aligned} & u+v=160 \\ & u=160-v \ldots \ldots(2) \\ & \text { Substitute (2) into (1) } \\ & v(160-v)=30(160-v)+30 v \\ & 160 v-v^2=4800-30 v+30 v \\ & v^2-160 v+4800=0 \\ &(v-40)(v-120)=0 \\ & v=40 \mathrm{~cm}, v=120 \mathrm{~cm} \end{aligned} $$
Therefore, the convex lens is located 40 cm or 120 cm from the screen in order to produce a sharp image on it.
A small bulb is at a distance of 1.6 m from the screen and a thin convex lens with a focal length of 30 cm is placed between the bulb and the screen. Determine two positions of the convex lens that can produce a sharp image on the screen.
Answer:

$$ f=30 \mathrm{~cm}, \quad u=+, v=+ \text { (convex lens) } $$
$$ \begin{aligned} &\text { Thin lens formula, }\\ &\begin{aligned} \frac{1}{f} & =\frac{1}{u}+\frac{1}{v} \\ \frac{1}{f} & =\frac{u+v}{v u} \\ \frac{1}{30} & =\frac{u+v}{v u} \\ v u & =30 u+30 v \ldots(1) \end{aligned} \end{aligned} $$
$$ \begin{aligned} & u+v=160 \\ & u=160-v \ldots \ldots(2) \\ & \text { Substitute (2) into (1) } \\ & v(160-v)=30(160-v)+30 v \\ & 160 v-v^2=4800-30 v+30 v \\ & v^2-160 v+4800=0 \\ &(v-40)(v-120)=0 \\ & v=40 \mathrm{~cm}, v=120 \mathrm{~cm} \end{aligned} $$
Therefore, the convex lens is located 40 cm or 120 cm from the screen in order to produce a sharp image on it.
