Question 1:
What phenomenon of waves happens when sea waves are approaching the beach? Explain your answer with the help of a diagram.
Answer:
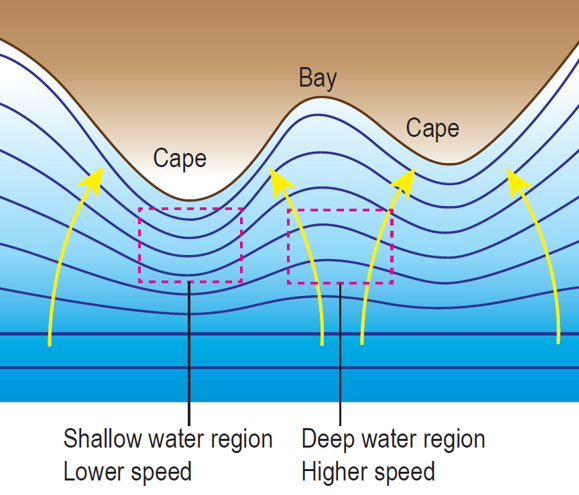
The phenomenon of refraction of sea waves :
– When the wavefront of the water propagates to the cape, the speed of the water waves decreases causing the wavelength to be shorter.
– Wavefront of water approaching the bay moves at a higher speed and the wavelength is longer.
– This causes the wavefront to curve and follow the shape of the shoreline.
– Refraction of water waves causes water wave energy to converge towards the cape. Water wave energy diverges from the bay and spread out to a wider region. Thus, the amplitude of waves at bay is smaller than at the cape.
What phenomenon of waves happens when sea waves are approaching the beach? Explain your answer with the help of a diagram.
Answer:

The phenomenon of refraction of sea waves :
– When the wavefront of the water propagates to the cape, the speed of the water waves decreases causing the wavelength to be shorter.
– Wavefront of water approaching the bay moves at a higher speed and the wavelength is longer.
– This causes the wavefront to curve and follow the shape of the shoreline.
– Refraction of water waves causes water wave energy to converge towards the cape. Water wave energy diverges from the bay and spread out to a wider region. Thus, the amplitude of waves at bay is smaller than at the cape.
Question 2:
Figure 5.44 shows plane water waves of frequency 10.0 Hz propagating from deep region to the boundary of shallow region PQ. Speed of the water wave in the deep region is 30 cm s–1.
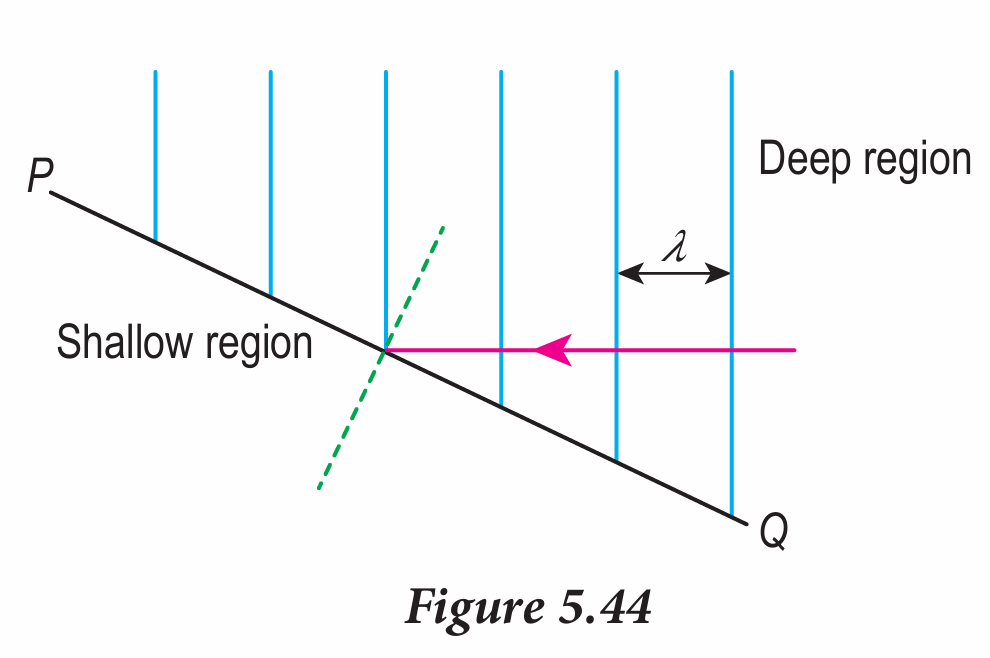
(a) Calculate the wavelength, λ.
(b) Calculate the speed of the water wave in the shallow region if the wavelength in this region is 1.5 cm.
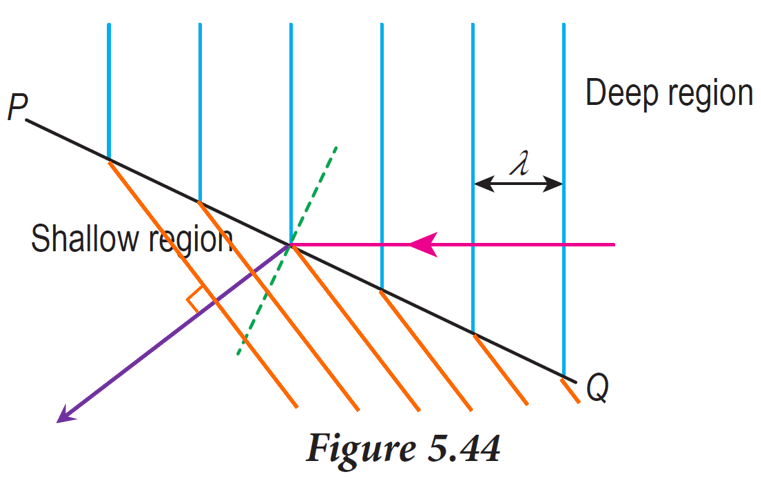
(c) Using arrows, draw the direction of propagation of the wave in the shallow region and then sketch the wavefronts of water waves refracted in this region.
(d) Compare frequency, wavelength and speed in the deep and shallow regions.
Answer:
$$ \begin{aligned} f & =10 \mathrm{~Hz} \\ v_1 & =30 \mathrm{~cm} \mathrm{~s}^{-1} \\ \lambda_1 & =? \\ \lambda_2 & =1.5 \mathrm{~cm} \\ v_2 & =? \end{aligned} $$
(a)
$$ \begin{aligned} v & =f \lambda \\ \lambda_1 & =\frac{v_1}{f} \\ \lambda_1 & =\frac{30}{10} \\ & =3 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} v & =f \lambda \\ v_2 & =f \lambda_2 \\ v_2 & =10 \times 1.5 \\ v_2 & =15 \mathrm{~cm} \mathrm{~s}^{-1} \end{aligned} $$
(c)
(d)
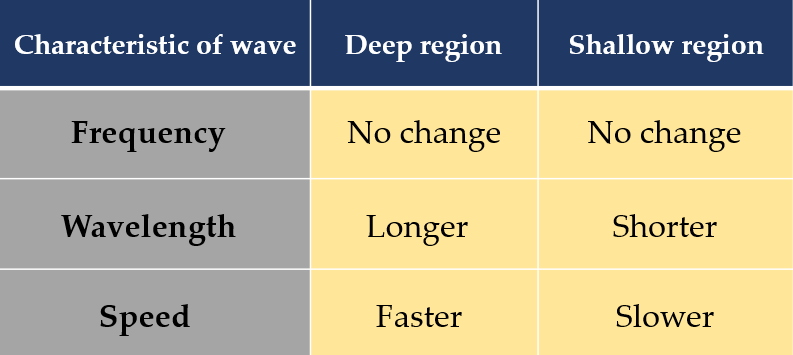
Figure 5.44 shows plane water waves of frequency 10.0 Hz propagating from deep region to the boundary of shallow region PQ. Speed of the water wave in the deep region is 30 cm s–1.

(a) Calculate the wavelength, λ.
(b) Calculate the speed of the water wave in the shallow region if the wavelength in this region is 1.5 cm.
(c) Using arrows, draw the direction of propagation of the wave in the shallow region and then sketch the wavefronts of water waves refracted in this region.
(d) Compare frequency, wavelength and speed in the deep and shallow regions.
Answer:
$$ \begin{aligned} f & =10 \mathrm{~Hz} \\ v_1 & =30 \mathrm{~cm} \mathrm{~s}^{-1} \\ \lambda_1 & =? \\ \lambda_2 & =1.5 \mathrm{~cm} \\ v_2 & =? \end{aligned} $$
(a)
$$ \begin{aligned} v & =f \lambda \\ \lambda_1 & =\frac{v_1}{f} \\ \lambda_1 & =\frac{30}{10} \\ & =3 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} v & =f \lambda \\ v_2 & =f \lambda_2 \\ v_2 & =10 \times 1.5 \\ v_2 & =15 \mathrm{~cm} \mathrm{~s}^{-1} \end{aligned} $$
(c)

(d)

