Question 1:
Figure 5.67 shows Young’s double-slit experiment.
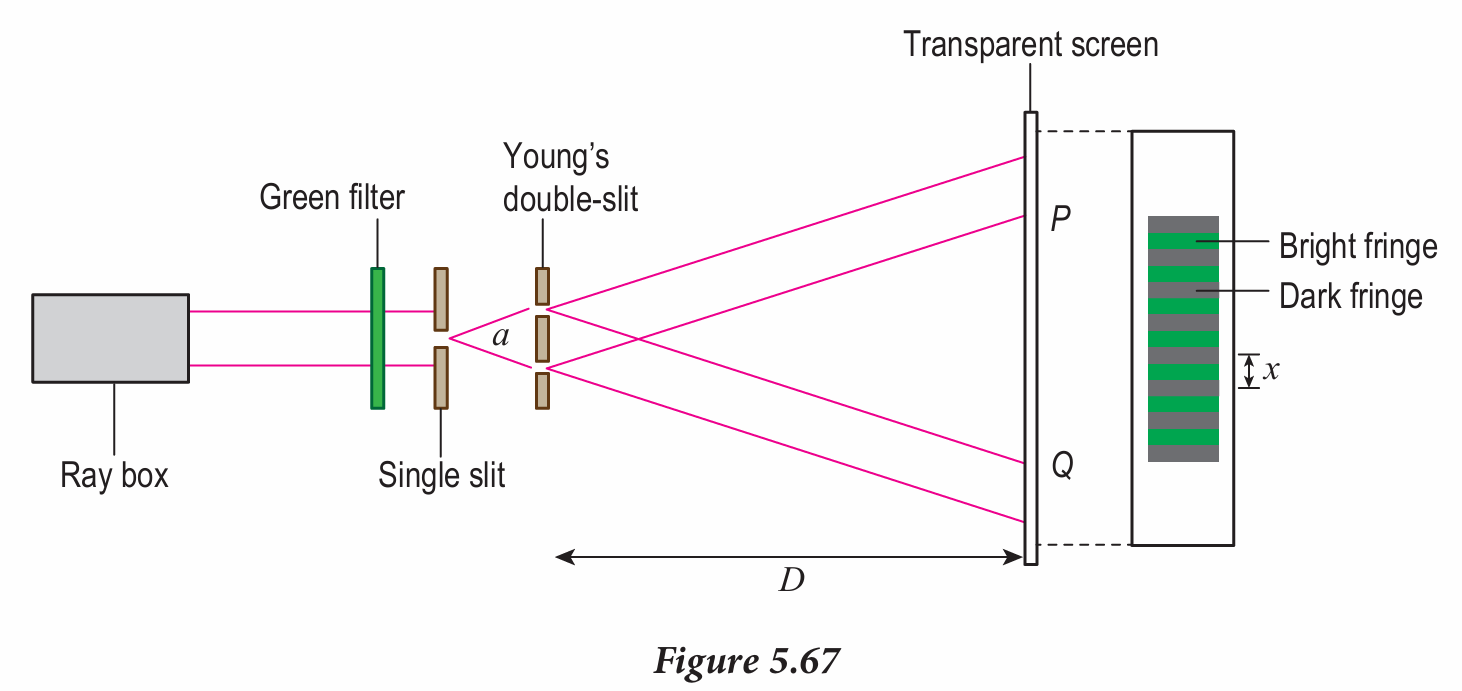
(a) State the phenomenon that occurs when light passes through the single slit.
(b) What will happen to the two light rays in the area PQ on the screen?
(c) Describe the formation of bright fringes and dark fringes.
(d) In the apparatus set up of this experiment, a = 0.30 mm, D = 2.5 m and x = 4.6 mm.
Calculate the wavelength, λ of the green light.
Answer:
(a) Diffraction
(b) An interference pattern is produced as a result of the superposition of two light waves emerging from the double slit.
(c)
The bright fringes are regions where constructive interference occurs.
The dark fringes are regions where destructive interference occurs.
(d)
$$ \begin{aligned} & a=0.30 \mathrm{~mm}=\left(0.30 \times 10^{-3}\right) \mathrm{m} \\ & x=4.6 \mathrm{~mm}=\left(4.6 \times 10^{-3}\right) \mathrm{m} \\ & D=2.5 \mathrm{~m} \\ & \lambda=? \end{aligned} $$
$$ \begin{aligned} \lambda & =\frac{a x}{D} \\ & =\frac{\left(0.30 \times 10^{-3}\right) \mathrm{m} \times\left(4.6 \times 10^{-3}\right) \mathrm{m}}{2.5 \mathrm{~m}} \\ & =5.52 \times 10^{-7} \mathrm{~m} \end{aligned} $$
Figure 5.67 shows Young’s double-slit experiment.

(a) State the phenomenon that occurs when light passes through the single slit.
(b) What will happen to the two light rays in the area PQ on the screen?
(c) Describe the formation of bright fringes and dark fringes.
(d) In the apparatus set up of this experiment, a = 0.30 mm, D = 2.5 m and x = 4.6 mm.
Calculate the wavelength, λ of the green light.
Answer:
(a) Diffraction
(b) An interference pattern is produced as a result of the superposition of two light waves emerging from the double slit.
(c)
The bright fringes are regions where constructive interference occurs.
The dark fringes are regions where destructive interference occurs.
(d)
$$ \begin{aligned} & a=0.30 \mathrm{~mm}=\left(0.30 \times 10^{-3}\right) \mathrm{m} \\ & x=4.6 \mathrm{~mm}=\left(4.6 \times 10^{-3}\right) \mathrm{m} \\ & D=2.5 \mathrm{~m} \\ & \lambda=? \end{aligned} $$
$$ \begin{aligned} \lambda & =\frac{a x}{D} \\ & =\frac{\left(0.30 \times 10^{-3}\right) \mathrm{m} \times\left(4.6 \times 10^{-3}\right) \mathrm{m}}{2.5 \mathrm{~m}} \\ & =5.52 \times 10^{-7} \mathrm{~m} \end{aligned} $$
