Question 3:
Figure 3 shows superposition of two coherent plane waves.
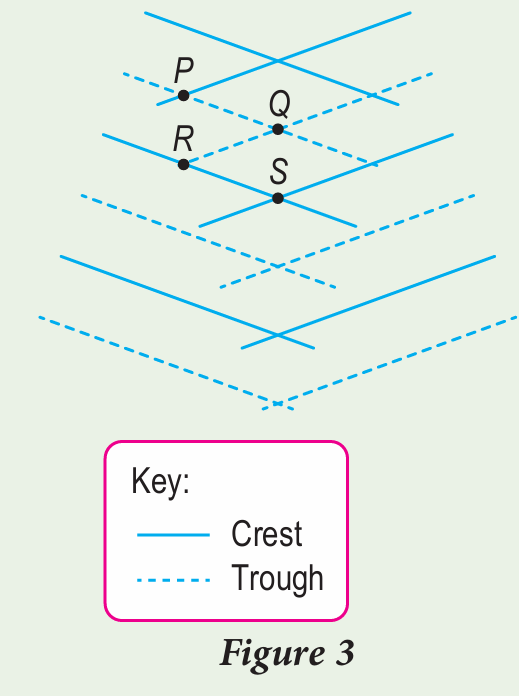
(a) What is a coherent wave?
(b) State the points where the following occur
(i) constructive interference,
(ii) destructive interference.
(c) Explain with suitable diagrams, interference at point
(i) Q,
(ii) R, and
(iii) S.
Answer:
(a)
Coherent waves are waves that have:
– same frequency
– constant phase difference
(b)(i)
Constructive interference occurs when two crests are in superposition.
Constructive interference also occurs when two troughs are in superposition.
Therefore, constructive interference occurs at point Q and point S.
(b)(ii)
Destructive interference occurs when a crest and a trough are in superposition to produce zero combined displacement.
Therefore, destructive interference occurs at point P and point R.
(c)(i)
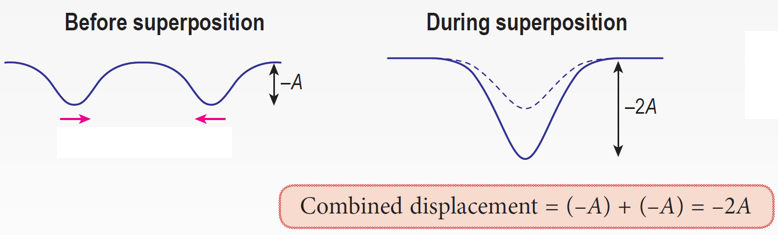
At point Q, constructive interference between two troughs.
(c)(ii)
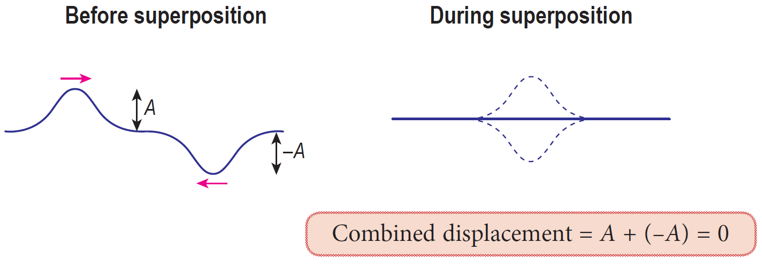
At point R, destructive interference between a crest and a trough.
(c)(iii)
At point S, constructive interference between two crests.
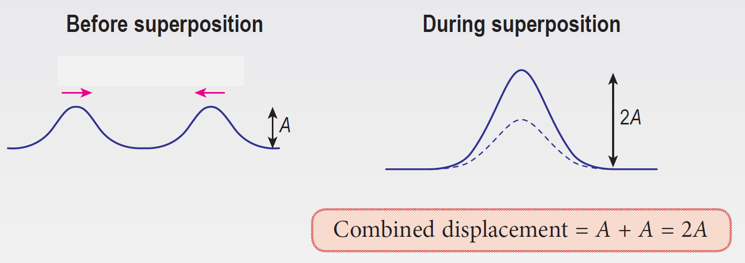
Figure 3 shows superposition of two coherent plane waves.

(a) What is a coherent wave?
(b) State the points where the following occur
(i) constructive interference,
(ii) destructive interference.
(c) Explain with suitable diagrams, interference at point
(i) Q,
(ii) R, and
(iii) S.
Answer:
(a)
Coherent waves are waves that have:
– same frequency
– constant phase difference
(b)(i)
Constructive interference occurs when two crests are in superposition.
Constructive interference also occurs when two troughs are in superposition.
Therefore, constructive interference occurs at point Q and point S.
(b)(ii)
Destructive interference occurs when a crest and a trough are in superposition to produce zero combined displacement.
Therefore, destructive interference occurs at point P and point R.
(c)(i)
At point Q, constructive interference between two troughs.

(c)(ii)
At point R, destructive interference between a crest and a trough.

(c)(iii)
At point S, constructive interference between two crests.

Question 4:
Figure 4 shows the apparatus set up of Young’s double-slit experiment.
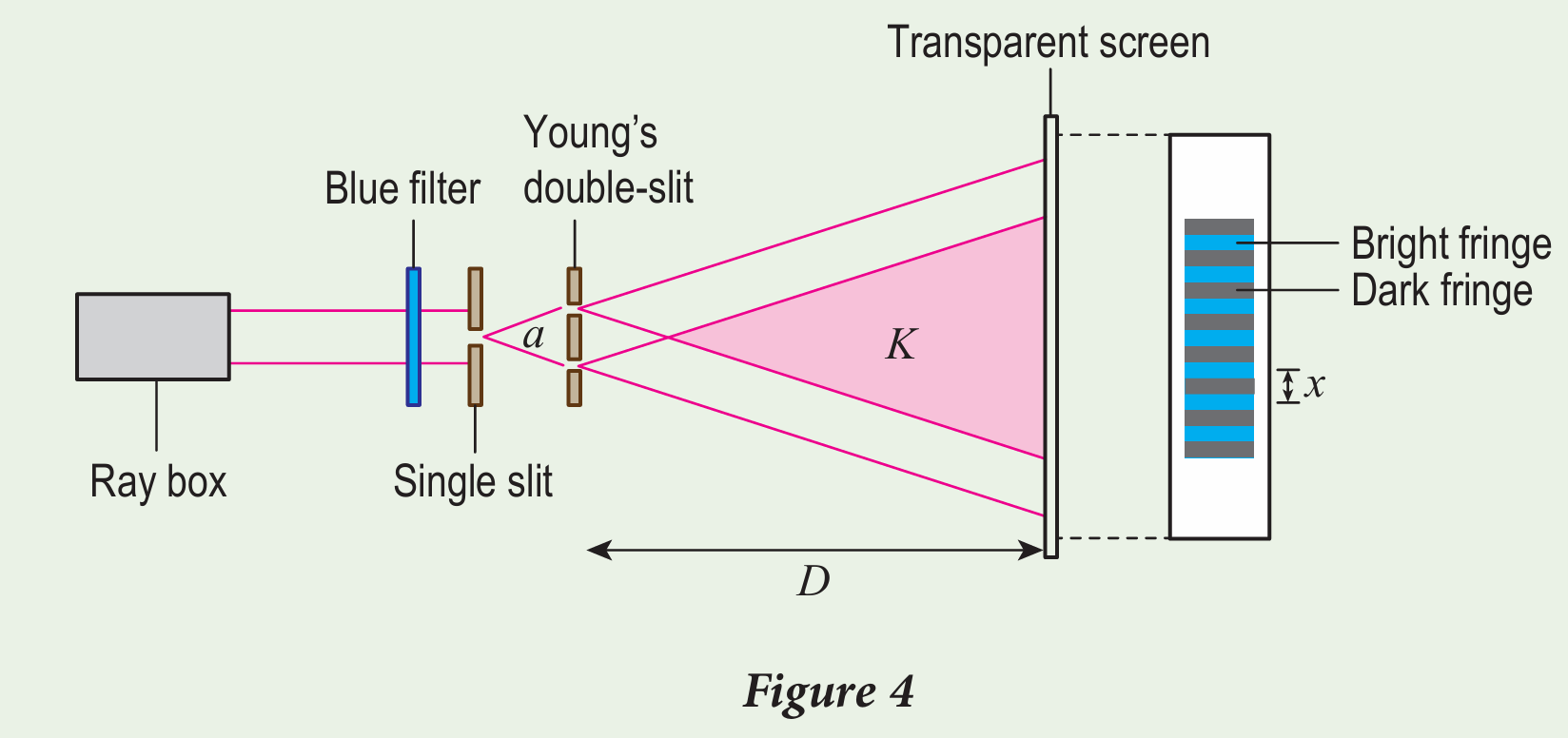
(a) What happens to the light rays at area K?
(b) Explain the formation of bright fringes and dark fringes on the screen.
(c) You are given the following information:
• Distance between double slits, a = 0.30 mm
• Distance between double-slits and screen, D = 2.70 m
• Separation distance between two adjacent bright fringes, x = 4.0 mm
Calculate the wavelength, λ of blue light in this experiment.
Answer:
(a) Superposition of waves/ Interference
(b)
Bright fringes are formed when waves undergo constructive interference.
Dark fringes are formed when waves undergo destructive interference.
(c)
$$ \begin{aligned} a & =0.30 \mathrm{~mm}=\left(0.30 \times 10^{-3}\right) \mathrm{m} \\ x & =4.0 \mathrm{~mm}=\left(4.0 \times 10^{-3}\right) \mathrm{m} \\ D & =2.70 \mathrm{~m} \\ \lambda & =? \\ \lambda & =\frac{a x}{D} \\ & =\frac{\left(0.30 \times 10^{-3}\right) \mathrm{m} \times\left(4.0 \times 10^{-3}\right) \mathrm{m}}{2.70 \mathrm{~m}} \\ & =4.44 \times 10^{-7} \mathrm{~m} \end{aligned} $$
Figure 4 shows the apparatus set up of Young’s double-slit experiment.

(a) What happens to the light rays at area K?
(b) Explain the formation of bright fringes and dark fringes on the screen.
(c) You are given the following information:
• Distance between double slits, a = 0.30 mm
• Distance between double-slits and screen, D = 2.70 m
• Separation distance between two adjacent bright fringes, x = 4.0 mm
Calculate the wavelength, λ of blue light in this experiment.
Answer:
(a) Superposition of waves/ Interference
(b)
Bright fringes are formed when waves undergo constructive interference.
Dark fringes are formed when waves undergo destructive interference.
(c)
$$ \begin{aligned} a & =0.30 \mathrm{~mm}=\left(0.30 \times 10^{-3}\right) \mathrm{m} \\ x & =4.0 \mathrm{~mm}=\left(4.0 \times 10^{-3}\right) \mathrm{m} \\ D & =2.70 \mathrm{~m} \\ \lambda & =? \\ \lambda & =\frac{a x}{D} \\ & =\frac{\left(0.30 \times 10^{-3}\right) \mathrm{m} \times\left(4.0 \times 10^{-3}\right) \mathrm{m}}{2.70 \mathrm{~m}} \\ & =4.44 \times 10^{-7} \mathrm{~m} \end{aligned} $$
