Question 5:
Seorang murid menggetarkan suatu spring slinki pada frekuensi 5 Hz supaya gelombang melintang yang terhasil adalah seperti yang ditunjukkan dalam Rajah 5.
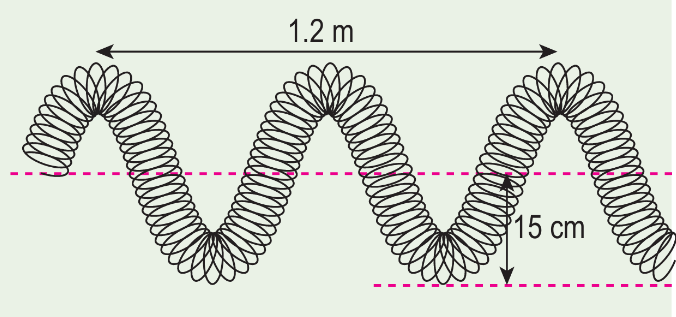
(a) Determine the amplitude, period and wavelength of the wave.
(b) Calculate the wave speed along the slinky spring.
Answer:
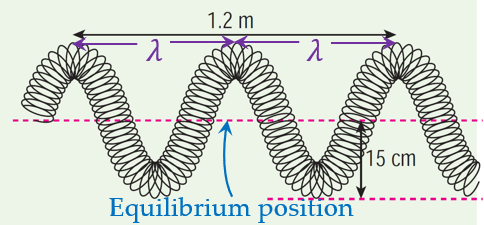
(a)
Amplitude is the maximum displacement from its equilibrium position.
∴ Amplitude = 15 cm
$$ \begin{aligned} &\begin{aligned} \text { Period } & =\frac{1}{f} \\ & =\frac{1}{5} \\ & =0.2 \mathrm{~s} \end{aligned}\\ &\begin{aligned} 2 \lambda & =1.2 \mathrm{~m} \\ \lambda & =\frac{1.2 \mathrm{~m}}{2} \\ & =0.6 \mathrm{~m} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} f & =5 \mathrm{~Hz} \\ v & =f \lambda \\ v & =5 \times 0.6 \\ & =3.0 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
Seorang murid menggetarkan suatu spring slinki pada frekuensi 5 Hz supaya gelombang melintang yang terhasil adalah seperti yang ditunjukkan dalam Rajah 5.

(a) Determine the amplitude, period and wavelength of the wave.
(b) Calculate the wave speed along the slinky spring.
Answer:

(a)
Amplitude is the maximum displacement from its equilibrium position.
∴ Amplitude = 15 cm
$$ \begin{aligned} &\begin{aligned} \text { Period } & =\frac{1}{f} \\ & =\frac{1}{5} \\ & =0.2 \mathrm{~s} \end{aligned}\\ &\begin{aligned} 2 \lambda & =1.2 \mathrm{~m} \\ \lambda & =\frac{1.2 \mathrm{~m}}{2} \\ & =0.6 \mathrm{~m} \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} f & =5 \mathrm{~Hz} \\ v & =f \lambda \\ v & =5 \times 0.6 \\ & =3.0 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
Question 6:
A judge blew a whistle which produced a sound of frequency 500 Hz and a wavelength of 0.67 m in the air. What is the wave speed of the sound?
Answer:
$$ \begin{aligned} f & =500 \mathrm{~Hz} \\ \lambda & =0.67 \mathrm{~m} \\ v & =f \lambda \\ & =500 \times 0.67 \\ & =335 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
A judge blew a whistle which produced a sound of frequency 500 Hz and a wavelength of 0.67 m in the air. What is the wave speed of the sound?
Answer:
$$ \begin{aligned} f & =500 \mathrm{~Hz} \\ \lambda & =0.67 \mathrm{~m} \\ v & =f \lambda \\ & =500 \times 0.67 \\ & =335 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
Question 7:
Figure 6 shows a tuning fork vibrating and producing sound waves.
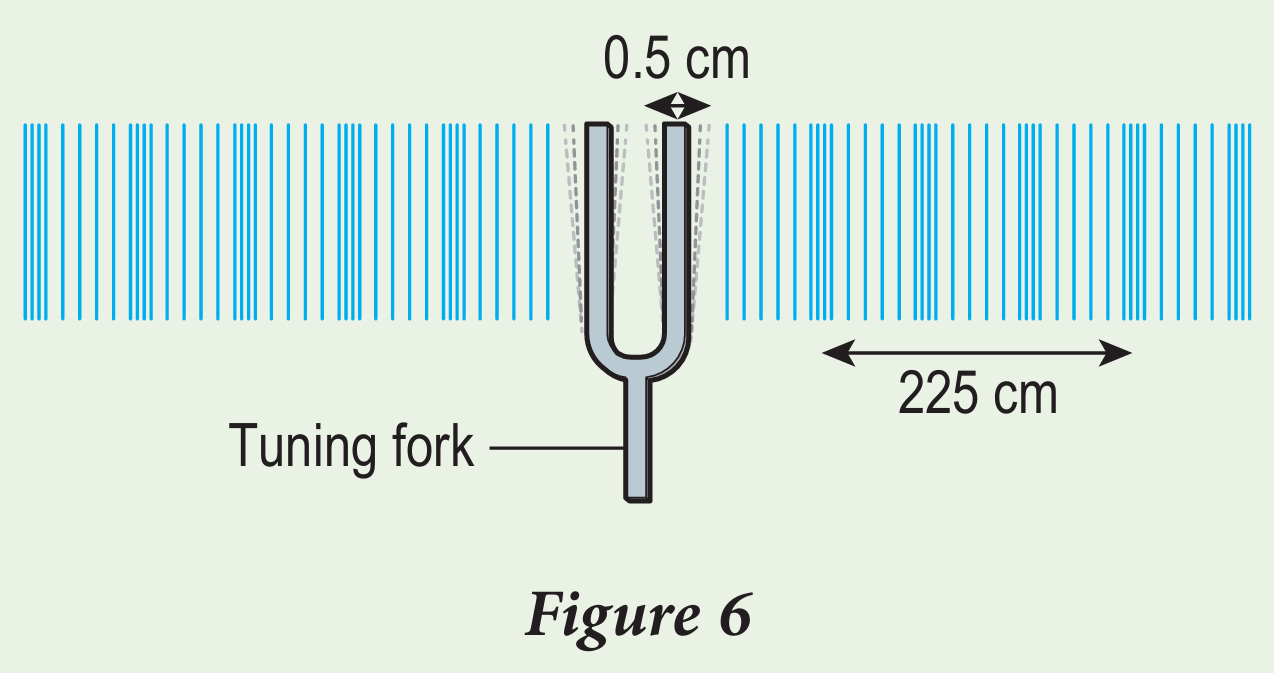
Based on Figure 6, determine the
(a) amplitude of the soun
d waves,
(b) wavelength of the sound waves,
(c) speed of the sound waves produced when the tuning fork vibrates with a frequency of 440 Hz.
Answer:
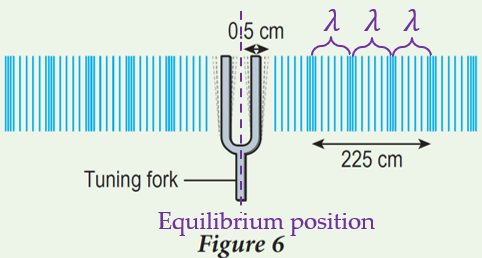
(a)
$$ \begin{aligned} \text { Amplitude } & =\frac{0.5}{2} \\ & =0.25 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} 3 \lambda & =225 \\ \lambda & =\frac{225}{3} \\ & =75 \mathrm{~cm} \end{aligned} $$
(c)
$$ \begin{aligned} f & =440 \mathrm{~Hz} \\ v & =f \lambda \\ & =440 \times 75 \\ & =33000 \mathrm{~cm} \mathrm{~s}^{-1} \end{aligned} $$
Figure 6 shows a tuning fork vibrating and producing sound waves.

Based on Figure 6, determine the
(a) amplitude of the soun
d waves,
(b) wavelength of the sound waves,
(c) speed of the sound waves produced when the tuning fork vibrates with a frequency of 440 Hz.
Answer:

(a)
$$ \begin{aligned} \text { Amplitude } & =\frac{0.5}{2} \\ & =0.25 \mathrm{~cm} \end{aligned} $$
(b)
$$ \begin{aligned} 3 \lambda & =225 \\ \lambda & =\frac{225}{3} \\ & =75 \mathrm{~cm} \end{aligned} $$
(c)
$$ \begin{aligned} f & =440 \mathrm{~Hz} \\ v & =f \lambda \\ & =440 \times 75 \\ & =33000 \mathrm{~cm} \mathrm{~s}^{-1} \end{aligned} $$
