Measuring e.m.f. and Internal Resistance
Three methods can be used to measure the e.m.f. and internal resistance.
Open Circuit – Closed Circuit
Open Circuit
In open circuit ( when the switch is off), the voltmeter shows the reading of the e.m.f.
Close Circuit
In close circuit ( when the switch is on), the voltmeter shows the reading of the potential difference across the cell.
With the presence of internal resistance, the potential difference across the cell is always less than the e.m.f.
Example 1:
The diagram above shows a simple circuit that connects some batteries to a resistor. The voltmeter shows a reading of 5.0V when the switch is off and 4.5V when the switch is on. What is the e.m.f. and the internal resistance of the cell?
Answer:
When the switch is off, the reading of the voltmeter shows the e.m.f. of the batteries. Therefore.
e.m.f. = 5.0V
When the switch is turned on, the reading of the voltmeter shows the potential difference of the resistor. Therefore,
V = 4.5V
The current that passes through the resistor,
I= V/R
I = 4.5/9
I = 0.5A
E=V+Ir
(5.0)=(4.5)+(0.5)r
0.5r=5.0−4.5
0.5r = 0.5
r= 0.5/0.5 =1Ω
Example 2:
 |
| Diagram (a) |
 |
| Diagram (b) |
A cell is connected to a circuit as shown in diagram (a). The graph in diagram (b) shows the change of the reading of the voltmeter, V against time, t. If t is the time where the switch is closed, find
(a) the e.m.f. of the cell
(b) the internal resistance of the cell.
Answer:
(a) Before the switch turned on, the reading of the ammeter shows the e.m.f. of the cells.
From the graph, the e.m.f. = 3.0V
(b)
e.m.f., E = 3.0V
Potential difference across the resistor, V = 2.5V
Current that pass through the resistor,
I= V/R
I = 2.5/2 =1.25A
E = V+Ir
(3.0) = (2.5)+(1.25)r
1.25r = 3.0−2.5 = 0.5
r= 0.5/1.25
r = 0.4Ω
Simultaneous Equations
Example 1
When a 1Ω resistor is connected to the terminal of a cell, the current that flows through it is 8A. When the resistor is replaced by another resistor with resistance 4Ω, the current becomes 2⅔A. Find the
a. internal resistance of the cell
b. e.m.f. of the cell
Answer:
Experiment 1
R1 = 1Ω
I1 = 8A
E = IR+Ir
E = (8)(1)+(8)r
E−8r = 8 ——(1)
Experiment 2
R2 = 4Ω
I2 = 2⅔A
E=IR+Ir
E=(2⅔ )(4)+(2⅔ )r
3E−8r=32 ——(2)
Solve the simultaneous equation
E = 12V, r = 0.5Ω
The diagram on the left shows that the terminal potential difference of a batteries is 1.2V when a 4 Ω resistor is connected to it. The terminal potential become 1.45V when the resistor is replaced by another resistor of resistance 29Ω
Find the
a. internal resistance, r
b. e.m.f. of the batteries.
Answer:
Experiment 1
V1 = 1.2V
R1 = 4Ω
I= V/R
I= 1.2/4 =0.3A
E=V+Ir
E=1.2+0.3r
E−0.3r=1.2 ——(1)
Experiment 2
V2 = 1.45V
R2 = 29
I= V/R
I= 1.45/29 =0.05A
E=V+Ir
E=1.45+0.05r
E−0.05r=1.45 ——(1)
Solve the simultaneous equation
E = 1.5V, r = 1Ω
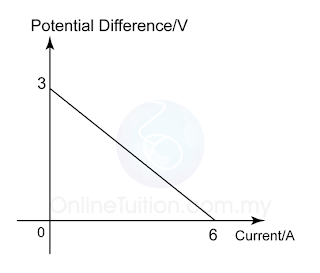
The Linear Graph
From the equation,
Therefore
Y axis = Potential difference (V)
X axis = Current (I)
Gradient od the grapf, m = – internal resistance (r)
Y intercept of the graph, c = e.m.f.
Example:
The graph shows the variation of potential difference with the current of a battery.
What is the internal resistance and e.m.f. of the battery?
Answer:
e.m.f. = y-intercept = 3V
internal resistance,
r = -gradient of the graph
r=− −3 6 =0.5Ω