Question 1:
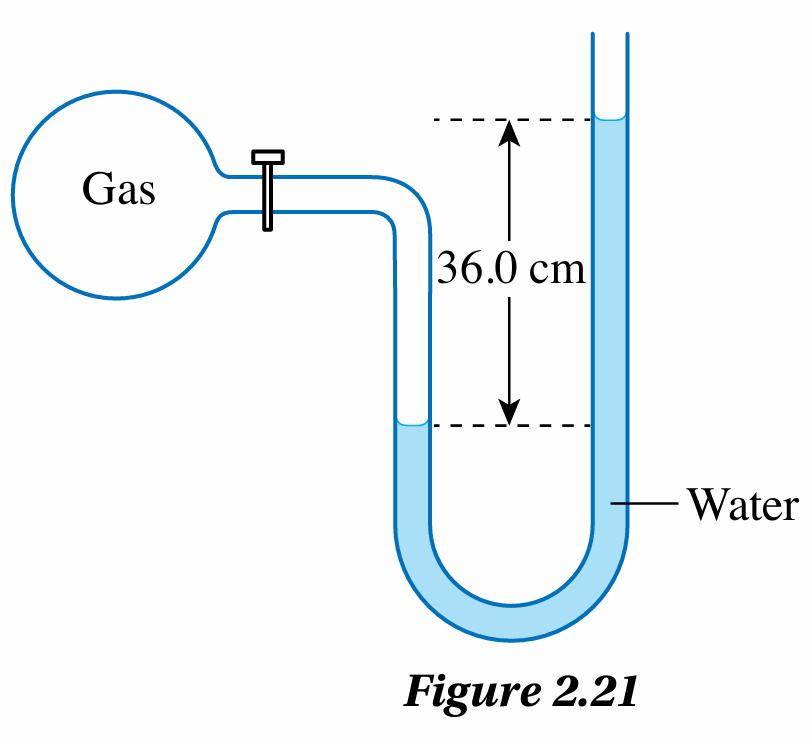
Figure 2.21 shows a water manometer connected to a flask containing gas.
(a) Compare the gas pressure in the flask with the atmospheric pressure.
(b) State the difference between the gas pressure and the atmospheric pressure in m H2O.
(c) Calculate the gas pressure in pascal.
[Density of water, ρ = 1 000 kg m–3 gravitational acceleration, g = 9.81 m s–2 and atmospheric pressure = 10.3 m H2O]
Answer:
(a)
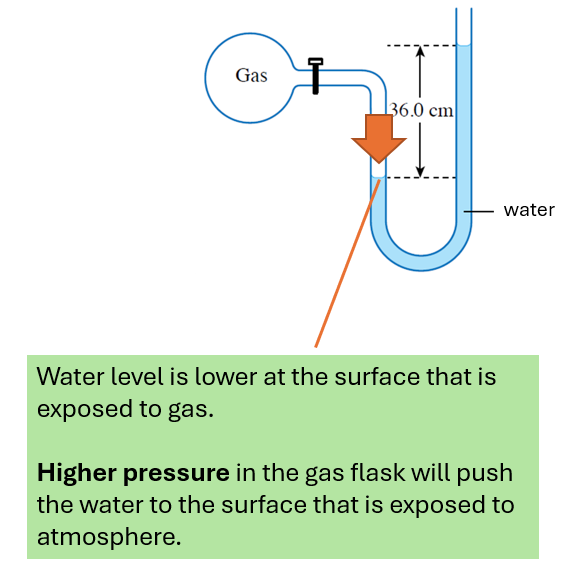The gas pressure is higher than the atmospheric pressure.
(b)
$$ \begin{aligned} & \text { Pressure difference } \\ & =\text { Difference of water level } \\ & =36.0 \mathrm{~cm} \mathrm{H}_2 \mathrm{O} \\ & =0.36 \mathrm{~m} \mathrm{H}_2 \mathrm{O} \end{aligned} $$
(c)
$$ \begin{aligned} & \text { Gas pressure (in unit } \left.\mathrm{m} \mathrm{H}_2 \mathrm{O}\right) \\ & =\text { water pressure }+ \text { atmospheric pressure } \\ & =(0.36+10.3) \\ & =10.66 \mathrm{~m} \mathrm{H}_2 \mathrm{O} \end{aligned} $$
$$ \begin{aligned} &\text { Gas pressure (in unit Pa) }\\ &\begin{aligned} & =h \rho g \\ & =(10.66) \times(1000) \times(9.81) \\ & =104575 \mathrm{~Pa} \end{aligned} \end{aligned} $$
Figure 2.21 shows a water manometer connected to a flask containing gas.
(a) Compare the gas pressure in the flask with the atmospheric pressure.
(b) State the difference between the gas pressure and the atmospheric pressure in m H2O.
(c) Calculate the gas pressure in pascal.
[Density of water, ρ = 1 000 kg m–3 gravitational acceleration, g = 9.81 m s–2 and atmospheric pressure = 10.3 m H2O]
Answer:
(a)
The gas pressure is higher than the atmospheric pressure.(b)
$$ \begin{aligned} & \text { Pressure difference } \\ & =\text { Difference of water level } \\ & =36.0 \mathrm{~cm} \mathrm{H}_2 \mathrm{O} \\ & =0.36 \mathrm{~m} \mathrm{H}_2 \mathrm{O} \end{aligned} $$
(c)
$$ \begin{aligned} & \text { Gas pressure (in unit } \left.\mathrm{m} \mathrm{H}_2 \mathrm{O}\right) \\ & =\text { water pressure }+ \text { atmospheric pressure } \\ & =(0.36+10.3) \\ & =10.66 \mathrm{~m} \mathrm{H}_2 \mathrm{O} \end{aligned} $$
$$ \begin{aligned} &\text { Gas pressure (in unit Pa) }\\ &\begin{aligned} & =h \rho g \\ & =(10.66) \times(1000) \times(9.81) \\ & =104575 \mathrm{~Pa} \end{aligned} \end{aligned} $$
Question 2:
What are the advantages of using a mercury manometer compared to a water manometer?
Answer:
– Can measure higher pressure because mercury is a denser liquid
– Does not need a very long tube
– Rate of evaporation of mercury is lower than rate of evaporation of water
What are the advantages of using a mercury manometer compared to a water manometer?
Answer:
– Can measure higher pressure because mercury is a denser liquid
– Does not need a very long tube
– Rate of evaporation of mercury is lower than rate of evaporation of water
Question 3:
A mercury manometer is connected to a steel cylinder containing compressed gas. The pressure of the compressed gas and the atmospheric pressure are 180 kPa and 101 kPa respectively. Calculate the difference in height between the two mercury columns in the manometer.
[Density of Hg, ρ = 13 600 kg m–3 and gravitational acceleration, g = 9.81 m s–2]
Answer:
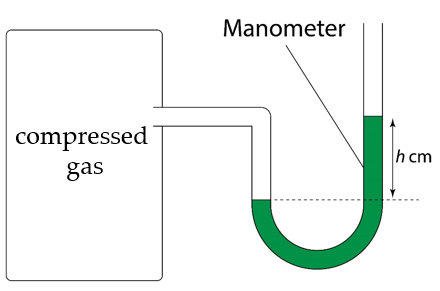
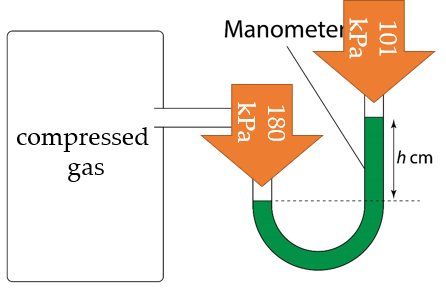
Difference in pressure between the compressed gas and atmospheric pressure
$$ \begin{aligned} & =180-101 \\ & =79 \mathrm{kPa} \\ & =79000 \mathrm{~Pa} \end{aligned} $$
$$ \begin{aligned} h \rho g & =79000 \\ h \times 13600 \times 9.81 & =79000 \\ h & =0.592 \mathrm{~m} \\ h & =59.2 \mathrm{~cm} \end{aligned} $$
Difference in height of the two mercury columns in the manometer = 59.2 cm
A mercury manometer is connected to a steel cylinder containing compressed gas. The pressure of the compressed gas and the atmospheric pressure are 180 kPa and 101 kPa respectively. Calculate the difference in height between the two mercury columns in the manometer.
[Density of Hg, ρ = 13 600 kg m–3 and gravitational acceleration, g = 9.81 m s–2]
Answer:
Difference in pressure between the compressed gas and atmospheric pressure
$$ \begin{aligned} & =180-101 \\ & =79 \mathrm{kPa} \\ & =79000 \mathrm{~Pa} \end{aligned} $$
$$ \begin{aligned} h \rho g & =79000 \\ h \times 13600 \times 9.81 & =79000 \\ h & =0.592 \mathrm{~m} \\ h & =59.2 \mathrm{~cm} \end{aligned} $$
Difference in height of the two mercury columns in the manometer = 59.2 cm