Question 11:
When a photodiode is shone on with a red light (λ = 700 nm) and a blue light (λ = 400 nm), the maximum kinetic energy of the photoelectrons emitted by the blue light is two times that of the red light.
(a) What is the work function of the photodiode?
(b) What is the threshold wavelength of the photodiode?
(c) What is the de Broglie wavelength of the photoelectron emitted by UV light (λ = 131 nm) from the photodiode?
Answer:
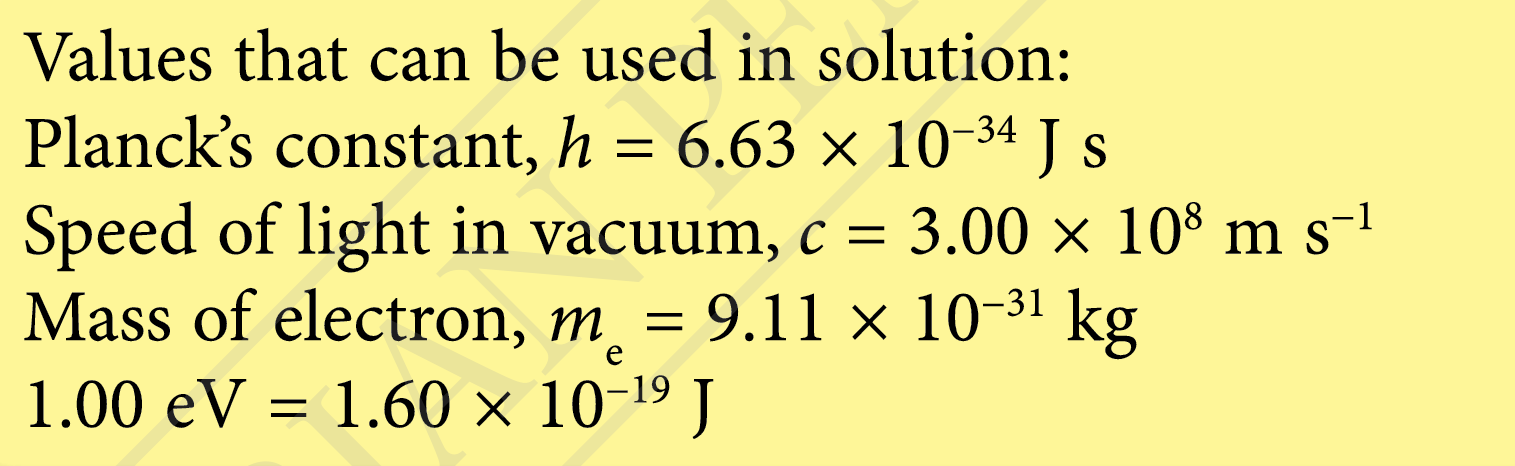
(a)
$$ \begin{aligned} &\text { Work function, } W\\ &\begin{aligned} & h f=W+K \\ & \frac{h c}{\lambda}=W+K \end{aligned} \end{aligned} $$
$$ \begin{gathered} \frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{700 \times 10^{-9}}=W+K \\ (\times 2) \Rightarrow 2 \times \frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{700 \times 10^{-9}}=2 W+2 K \ldots \end{gathered} $$
$$ \frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{400 \times 10^{-9}}=W+2 K \ldots \ldots .(2) $$
$$ \begin{aligned} &(1)-(2): \\ & W=2 \times \frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{700 \times 10^{-9}} \\ &-\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{400 \times 10^{-9}} \\ &=7.10 \times 10^{-20} \mathrm{~J} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Threshold wavelength, } \lambda_0\\ &\begin{aligned} \frac{h c}{\lambda_0} & =W \\ \lambda_0 & =\frac{h c}{W} \\ \lambda_0 & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{7.10 \times 10^{-20} \text { from }(\mathrm{a})} \\ & =2.80 \times 10^{-6} \mathrm{~m} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { de Broglie wavelength, } \lambda_{\mathrm{p}}\\ &\begin{aligned} \frac{h c}{\lambda} & =W+K_{\text {maks }} \\ K_{\text {maks }} & =\frac{h c}{\lambda}-W \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{131 \times 10^{-9}}-7.10 \times 10^{-20} \\ & =1.48 \times 10^{-18} \mathrm{~J} \end{aligned} \end{aligned} $$
$$ \begin{aligned} K & =\frac{1}{2} m v^2 \\ 2 K & =m v^2 \\ 2 m K & =m^2 v^2 \\ m v & =\sqrt{2 m K} \end{aligned} $$
$$ \begin{aligned} \lambda_{\mathrm{p}} & =\frac{h}{m_e v} \\ & =\frac{h}{\sqrt{2 m_{\mathrm{e}} K}} \\ & =\frac{6.63 \times 10^{-34}}{\sqrt{2\left(9.11 \times 10^{-31}\right)\left(1.48 \times 10^{-18}\right)}} \\ & =4.04 \times 10^{-10} \mathrm{~m} \end{aligned} $$
When a photodiode is shone on with a red light (λ = 700 nm) and a blue light (λ = 400 nm), the maximum kinetic energy of the photoelectrons emitted by the blue light is two times that of the red light.
(a) What is the work function of the photodiode?
(b) What is the threshold wavelength of the photodiode?
(c) What is the de Broglie wavelength of the photoelectron emitted by UV light (λ = 131 nm) from the photodiode?
Answer:
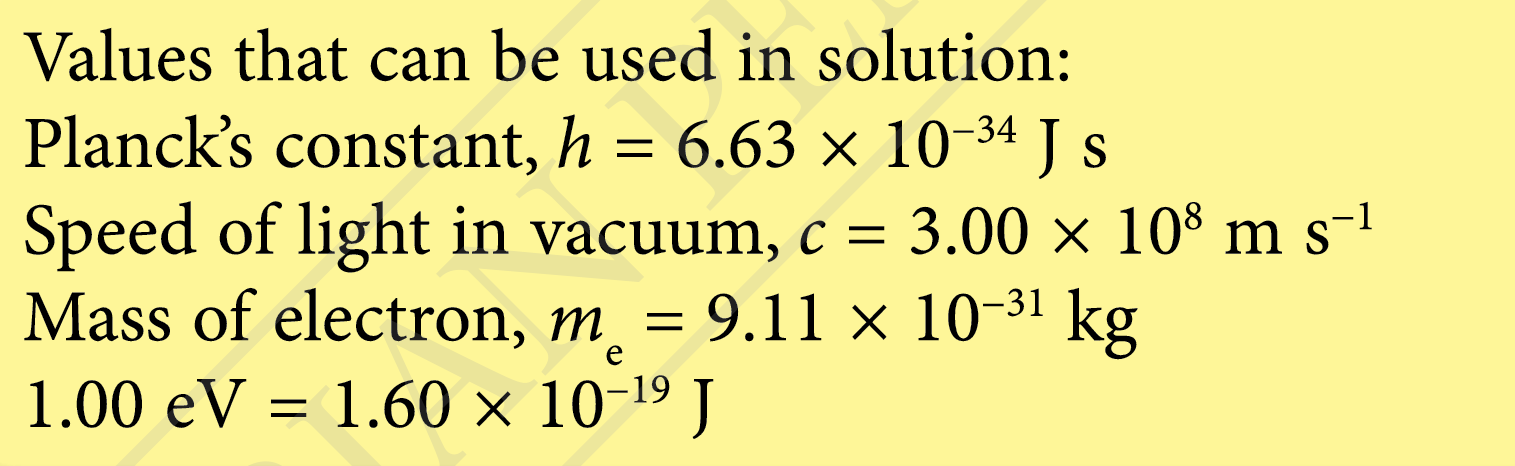
(a)
$$ \begin{aligned} &\text { Work function, } W\\ &\begin{aligned} & h f=W+K \\ & \frac{h c}{\lambda}=W+K \end{aligned} \end{aligned} $$
$$ \begin{gathered} \frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{700 \times 10^{-9}}=W+K \\ (\times 2) \Rightarrow 2 \times \frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{700 \times 10^{-9}}=2 W+2 K \ldots \end{gathered} $$
$$ \frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{400 \times 10^{-9}}=W+2 K \ldots \ldots .(2) $$
$$ \begin{aligned} &(1)-(2): \\ & W=2 \times \frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{700 \times 10^{-9}} \\ &-\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{400 \times 10^{-9}} \\ &=7.10 \times 10^{-20} \mathrm{~J} \end{aligned} $$
(b)
$$ \begin{aligned} &\text { Threshold wavelength, } \lambda_0\\ &\begin{aligned} \frac{h c}{\lambda_0} & =W \\ \lambda_0 & =\frac{h c}{W} \\ \lambda_0 & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{7.10 \times 10^{-20} \text { from }(\mathrm{a})} \\ & =2.80 \times 10^{-6} \mathrm{~m} \end{aligned} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { de Broglie wavelength, } \lambda_{\mathrm{p}}\\ &\begin{aligned} \frac{h c}{\lambda} & =W+K_{\text {maks }} \\ K_{\text {maks }} & =\frac{h c}{\lambda}-W \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{131 \times 10^{-9}}-7.10 \times 10^{-20} \\ & =1.48 \times 10^{-18} \mathrm{~J} \end{aligned} \end{aligned} $$
$$ \begin{aligned} K & =\frac{1}{2} m v^2 \\ 2 K & =m v^2 \\ 2 m K & =m^2 v^2 \\ m v & =\sqrt{2 m K} \end{aligned} $$
$$ \begin{aligned} \lambda_{\mathrm{p}} & =\frac{h}{m_e v} \\ & =\frac{h}{\sqrt{2 m_{\mathrm{e}} K}} \\ & =\frac{6.63 \times 10^{-34}}{\sqrt{2\left(9.11 \times 10^{-31}\right)\left(1.48 \times 10^{-18}\right)}} \\ & =4.04 \times 10^{-10} \mathrm{~m} \end{aligned} $$
