Question 12:
Amin conducted an experiment to determine the work function and threshold wavelength for a material X. The arrangement of the apparatus is as shown in Figure 2.
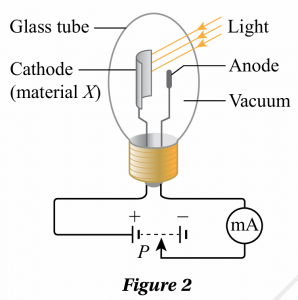
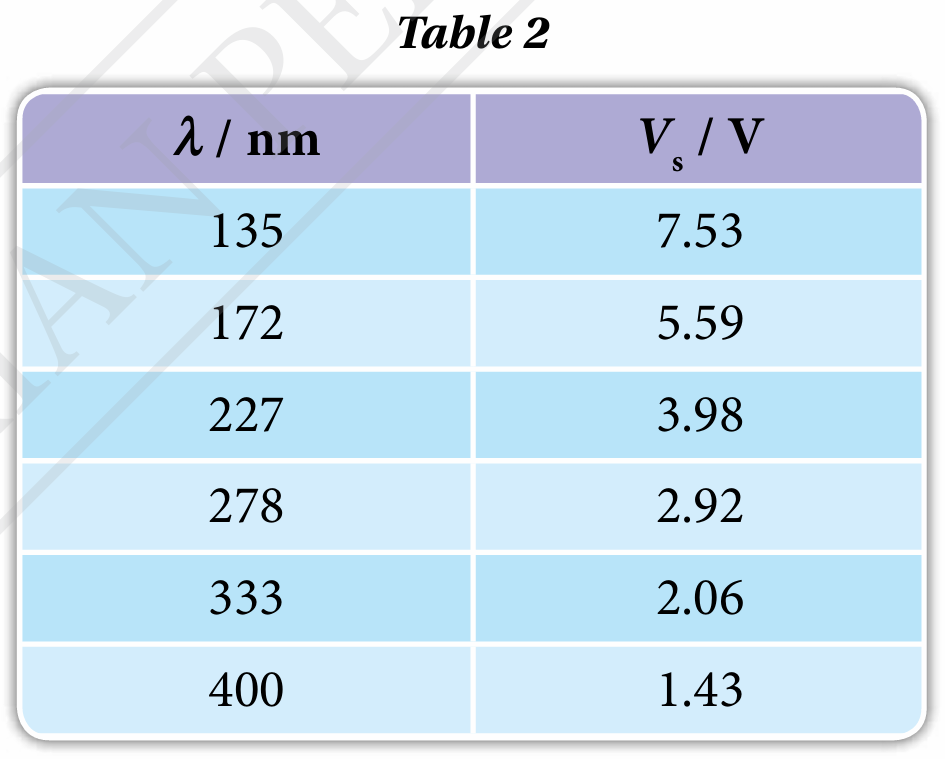
When the cathode coated with material X is illuminated by a light beam of wavelength, λ, the emitted photoelectrons will move towards the anode and give a reading in milliammeter. If the connection to the power supply is reversed, the potential difference at the anode is set to negative and that will prevent the arrival of the negatively charged photoelectrons. If the potential divider, P is adjusted until the stopping potential, Vs results in a zero milliammeter reading, then Vs is a measure of the maximum kinetic energy, Kmax of the photoelectrons emitted, of which Kmax = eVs. Table 2 shows the experimental results for the values of l and the corresponding values of Vs.
(a) Based on Einstein’s Photoelectric Equation, derive an equation that relates λ and Vs.
(b) Plot a suitable graph to determine the Planck’s constant, work function and threshold wavelength for material X.
(c) Calculate the wavelength of light for the production of a 10.0 eV photoelectron using the work function in (b).
(d) What is the de Broglie wavelength for the 10.0 eV photoelectron?
(e) Why is material X a critical component in a night vision device?
Answer:
(a)
$$ \begin{aligned} &\text { Based on Einstein′s Photoelectric Equation, }\\ &\begin{aligned} h f & =W+K_{\text {max }} \\ h f & =W+e V_s, W=\frac{h c}{\lambda_0} \\ \frac{h c}{\lambda} & =\frac{h c}{\lambda_0}+e V_{\mathrm{s}} \\ e V_{\mathrm{s}} & =h\left(\frac{c}{\lambda}\right)-h\left(\frac{c}{\lambda_0}\right) \\ V_{\mathrm{s}} & =\frac{h c}{e}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right) \end{aligned} \end{aligned} $$
(b)
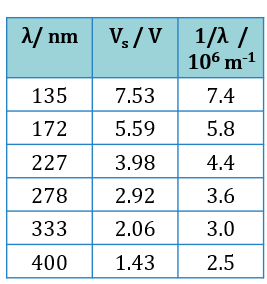
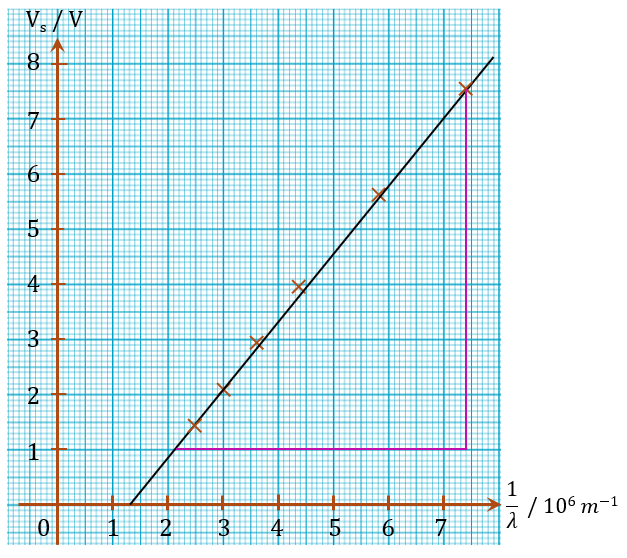
$$ \begin{aligned} & \text { Gradient of graph, } m \\ & =\frac{7.53-1.00}{(7.4-2.1) \times 10^6} \\ & =1.23 \times 10^{-6} \mathrm{~V} \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} h & =\frac{m e}{c} \\ & =\frac{\left(1.23 \times 10^{-6}\right)\left(1.60 \times 10^{-19}\right)}{3.00 \times 10^8} \\ & =6.56 \times 10^{-34} \mathrm{Js} \end{aligned} $$
$$ \begin{aligned} &\text {Threshold wavelength,}\\ &\begin{aligned} & \frac{1}{\lambda_0}=1.3 \times 10^6 \mathrm{~m}^{-1} \\ & \lambda_0=7.69 \times 10^{-7} \mathrm{~m} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text {Work function of,}\\ &\begin{aligned} X & =\frac{h c}{\lambda_0} \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{7.69 \times 10^{-7}} \\ & =2.59 \times 10^{-19} \mathrm{~J} \end{aligned} \end{aligned} $$
(c)
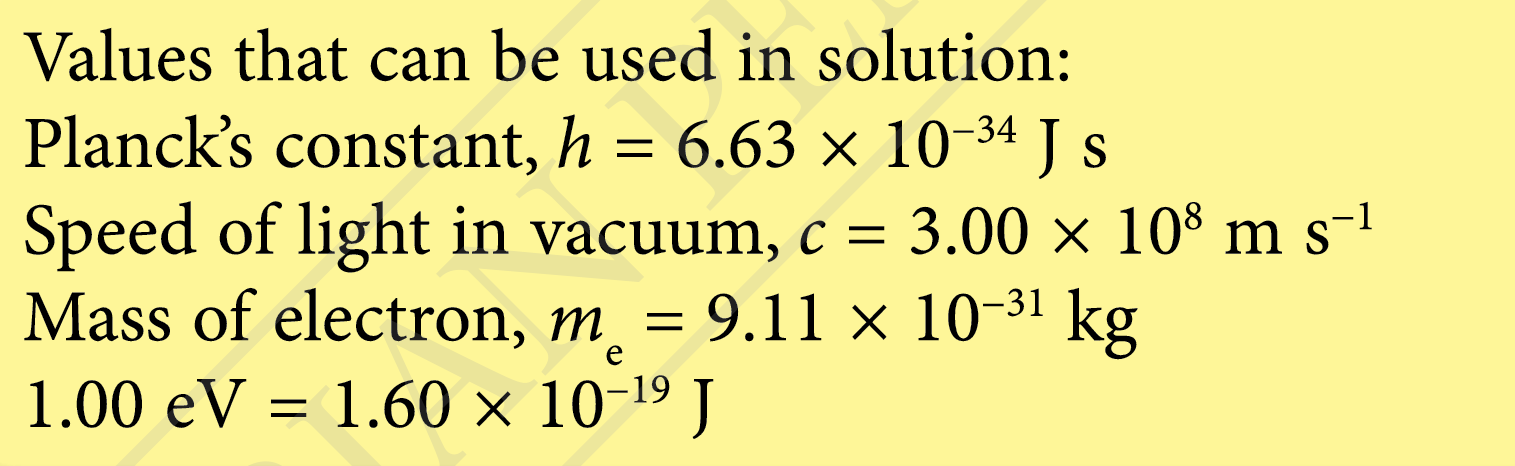
$$ \begin{aligned} \frac{h c}{\lambda} & =W+K_{\text {max }} \\ \lambda & =\frac{h c}{W+K_{\text {max }}} \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{2.59 \times 10^{-19}+\left(10.0 \times 1.60 \times 10^{-19}\right)} \\ & =1.07 \times 10^{-7} \mathrm{~m} \end{aligned} $$
(d)
$$ \begin{aligned} &\text { de Broglie wavelength, }\\ &\begin{aligned} \lambda_e & =\frac{h}{m_e v} \\ & =\frac{h}{\sqrt{2 m_{\mathrm{e}} K}} \\ & =\frac{6.63 \times 10^{-34}}{\sqrt{2\left(9.11 \times 10^{-31}\right)\left(10.0 \times 1.60 \times 10^{-19}\right)}} \\ & =3.88 \times 10^{-10} \mathrm{~m} \end{aligned} \end{aligned} $$
(e)
For a night vision device, X should have a threshold wavelength longer than that of visible light (4 ~ 7 × 10–7 m).
X has a threshold wavelength of 7.69 × 10–7 m, so it can be activated by radiation outside the wavelength of visible light and function in the dark.
Amin conducted an experiment to determine the work function and threshold wavelength for a material X. The arrangement of the apparatus is as shown in Figure 2.

When the cathode coated with material X is illuminated by a light beam of wavelength, λ, the emitted photoelectrons will move towards the anode and give a reading in milliammeter. If the connection to the power supply is reversed, the potential difference at the anode is set to negative and that will prevent the arrival of the negatively charged photoelectrons. If the potential divider, P is adjusted until the stopping potential, Vs results in a zero milliammeter reading, then Vs is a measure of the maximum kinetic energy, Kmax of the photoelectrons emitted, of which Kmax = eVs. Table 2 shows the experimental results for the values of l and the corresponding values of Vs.

(a) Based on Einstein’s Photoelectric Equation, derive an equation that relates λ and Vs.
(b) Plot a suitable graph to determine the Planck’s constant, work function and threshold wavelength for material X.
(c) Calculate the wavelength of light for the production of a 10.0 eV photoelectron using the work function in (b).
(d) What is the de Broglie wavelength for the 10.0 eV photoelectron?
(e) Why is material X a critical component in a night vision device?
Answer:
(a)
$$ \begin{aligned} &\text { Based on Einstein′s Photoelectric Equation, }\\ &\begin{aligned} h f & =W+K_{\text {max }} \\ h f & =W+e V_s, W=\frac{h c}{\lambda_0} \\ \frac{h c}{\lambda} & =\frac{h c}{\lambda_0}+e V_{\mathrm{s}} \\ e V_{\mathrm{s}} & =h\left(\frac{c}{\lambda}\right)-h\left(\frac{c}{\lambda_0}\right) \\ V_{\mathrm{s}} & =\frac{h c}{e}\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right) \end{aligned} \end{aligned} $$
(b)


$$ \begin{aligned} & \text { Gradient of graph, } m \\ & =\frac{7.53-1.00}{(7.4-2.1) \times 10^6} \\ & =1.23 \times 10^{-6} \mathrm{~V} \mathrm{~m} \end{aligned} $$
$$ \begin{aligned} h & =\frac{m e}{c} \\ & =\frac{\left(1.23 \times 10^{-6}\right)\left(1.60 \times 10^{-19}\right)}{3.00 \times 10^8} \\ & =6.56 \times 10^{-34} \mathrm{Js} \end{aligned} $$
$$ \begin{aligned} &\text {Threshold wavelength,}\\ &\begin{aligned} & \frac{1}{\lambda_0}=1.3 \times 10^6 \mathrm{~m}^{-1} \\ & \lambda_0=7.69 \times 10^{-7} \mathrm{~m} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text {Work function of,}\\ &\begin{aligned} X & =\frac{h c}{\lambda_0} \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{7.69 \times 10^{-7}} \\ & =2.59 \times 10^{-19} \mathrm{~J} \end{aligned} \end{aligned} $$
(c)
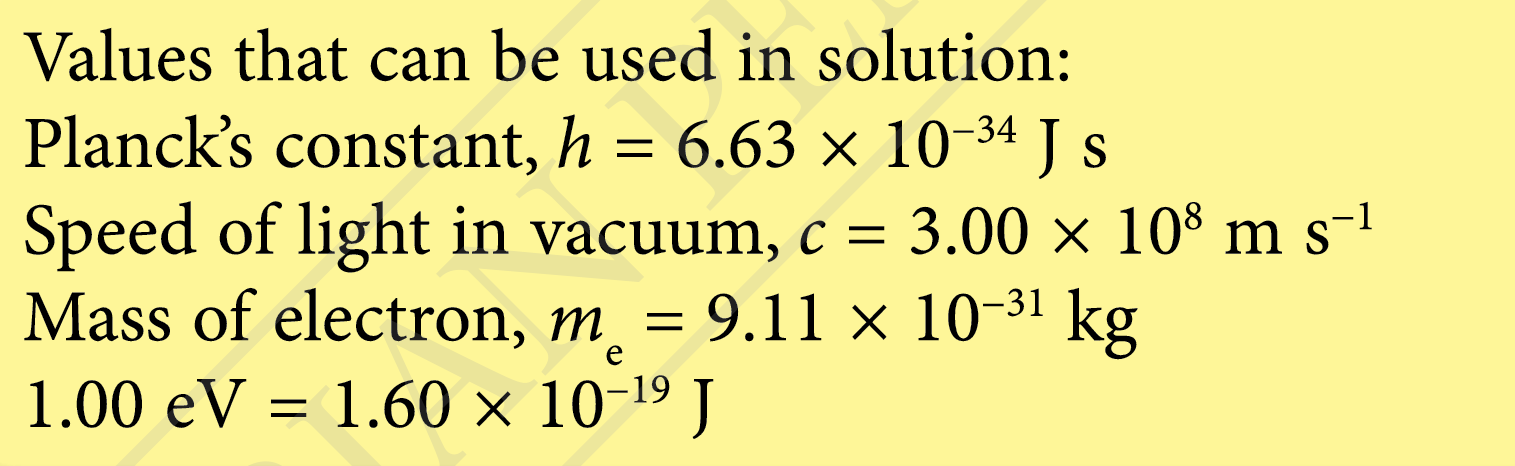
$$ \begin{aligned} \frac{h c}{\lambda} & =W+K_{\text {max }} \\ \lambda & =\frac{h c}{W+K_{\text {max }}} \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{2.59 \times 10^{-19}+\left(10.0 \times 1.60 \times 10^{-19}\right)} \\ & =1.07 \times 10^{-7} \mathrm{~m} \end{aligned} $$
(d)
$$ \begin{aligned} &\text { de Broglie wavelength, }\\ &\begin{aligned} \lambda_e & =\frac{h}{m_e v} \\ & =\frac{h}{\sqrt{2 m_{\mathrm{e}} K}} \\ & =\frac{6.63 \times 10^{-34}}{\sqrt{2\left(9.11 \times 10^{-31}\right)\left(10.0 \times 1.60 \times 10^{-19}\right)}} \\ & =3.88 \times 10^{-10} \mathrm{~m} \end{aligned} \end{aligned} $$
(e)
For a night vision device, X should have a threshold wavelength longer than that of visible light (4 ~ 7 × 10–7 m).
X has a threshold wavelength of 7.69 × 10–7 m, so it can be activated by radiation outside the wavelength of visible light and function in the dark.
