Question 9:
A hot air balloon is in a stationary position in the air.
(a) State Archimedes’ principle.
(b) Explain the relationship between the weight of the balloon and the weight of air displaced.
(c) When the flame of the burner is extinguished and the parachute valve is opened, the balloon begins to descend. Explain how this action enables the balloon to descend to the ground.
Answer:
(a) Archimedes’ principle states that an object which is partially or fully immersed in a fluid will experience a buoyant force equal to the weight of fluid displaced.
(b)
The balloon is stationary, that is the forces acting on the balloon are in equilibrium.
Resultant force on the balloon = 0.
Weight of balloon = buoyant force
According to Archimedes’ principle, buoyant force = weight of air displaced
Therefore, weight of balloon = weight of air displaced
(c)
When the flame of the burner is extinguished and the parachute valve is opened:
– part of the hot air in the balloon flows out through the valve
– temperature of the air in the balloon decreases
– cooler surrounding air flows into the balloon
– density of the balloon increases
– weight of the balloon increases
Since the weight of the balloon > buoyant force, there is a resultant force downwards
The balloon moves down until it reaches the ground.
A hot air balloon is in a stationary position in the air.
(a) State Archimedes’ principle.
(b) Explain the relationship between the weight of the balloon and the weight of air displaced.
(c) When the flame of the burner is extinguished and the parachute valve is opened, the balloon begins to descend. Explain how this action enables the balloon to descend to the ground.
Answer:
(a) Archimedes’ principle states that an object which is partially or fully immersed in a fluid will experience a buoyant force equal to the weight of fluid displaced.
(b)
The balloon is stationary, that is the forces acting on the balloon are in equilibrium.
Resultant force on the balloon = 0.
Weight of balloon = buoyant force
According to Archimedes’ principle, buoyant force = weight of air displaced
Therefore, weight of balloon = weight of air displaced
(c)
When the flame of the burner is extinguished and the parachute valve is opened:
– part of the hot air in the balloon flows out through the valve
– temperature of the air in the balloon decreases
– cooler surrounding air flows into the balloon
– density of the balloon increases
– weight of the balloon increases
Since the weight of the balloon > buoyant force, there is a resultant force downwards
The balloon moves down until it reaches the ground.
Question 10:
Figure 4 and Figure 5 show the same metal blocks of mass 0.050 kg hanging from a spring balance, immersed in water and cooking oil respectively.
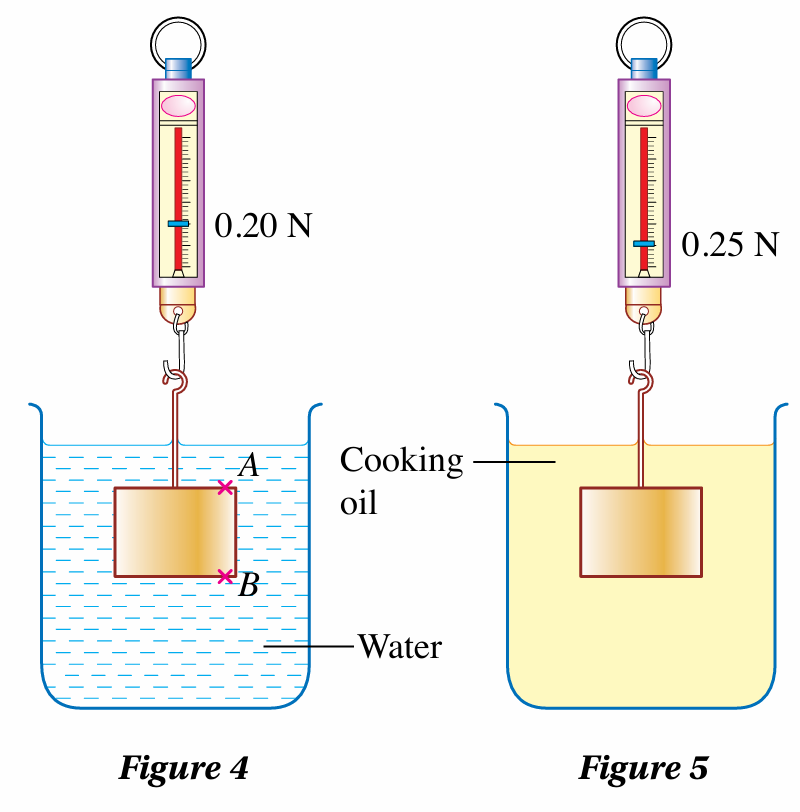
(a) Compare the pressure at point A and point B in Figure 4. Explain your answer.
(b) Explain how the difference in pressure in 10(a) exerts a buoyant force on the metal block.
(c) Calculate the density of cooking oil if the density of water is 1 000 kg m–3.
[Gravitational acceleration, g = 9.81 m s–2]
Answer:
(a)
Pressure at point A < pressure at point B
because the depth of A is lower than B
(b) Pressure on the lower surface of the metal block . pressure on the upper surface of the metal block
Force on the lower surface of the metal block . force on the upper surface of the metal block
A resultant force acts upwards.
This resultant force is the buoyant force.
(c)
$$ \begin{aligned} \text { Weight of block in air } & =m g \\ & =0.050 \times 9.81 \\ & =0.49 \mathrm{~N} \end{aligned} $$
$$ \begin{aligned} & \text { When the metal block is in water: } \\ & \text { Weight of metal block in water }=0.20 \mathrm{~N} \\ & \begin{aligned} \text { Apparent loss in weight of the metal block } & =0.49-0.20 \\ & =0.29 \mathrm{~N} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Buoyant force } & =\text { apparent loss in weight of the metal block } \\ & =0.29 \mathrm{~N} \end{aligned} $$
$$ \begin{aligned} &\text { Buoyant force, } F_{\mathrm{B}}=\rho V g \text {, }\\ &\begin{aligned} & \rho=\text { density of water } \\ & V=\text { volume of water displaced } \\ & \rho V g=0.29 \\ & 1000 \times V \times 9.81=0.29 \\ & V=2.96 \times 10^{-5} \mathrm{~m}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { When the block is in oil: } \\ & \begin{aligned} \text { Volume of oil displaced } & =\text { volume of water displaced } \\ & =2.96 \times 10^{-5} \mathrm{~m}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Weight of metal block in oil }=0.25 \mathrm{~N} \\ & \begin{aligned} \text { Apparent loss in weight of the metal block } & =0.49-0.25 \\ & =0.24 \mathrm{~N} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Buoyant force } & =\text { apparent loss in weight of the metal block } \\ & =0.24 \mathrm{~N} \end{aligned} $$
$$ \begin{aligned} & \text { Buoyant force, } F_{\mathrm{B}}=\rho V g, \\ & \rho=\text { density of oil } \\ & V=\text { volume of oil displaced } \\ & \quad \rho V g=0.24 \\ & \begin{aligned} \rho \times 2.96 \times 10^{-5} \times 9.81 & =0.24 \\ \quad \rho & =826.5 \mathrm{~kg} \mathrm{~m}^{-3} \end{aligned} \end{aligned} $$
Figure 4 and Figure 5 show the same metal blocks of mass 0.050 kg hanging from a spring balance, immersed in water and cooking oil respectively.

(a) Compare the pressure at point A and point B in Figure 4. Explain your answer.
(b) Explain how the difference in pressure in 10(a) exerts a buoyant force on the metal block.
(c) Calculate the density of cooking oil if the density of water is 1 000 kg m–3.
[Gravitational acceleration, g = 9.81 m s–2]
Answer:
(a)
Pressure at point A < pressure at point B
because the depth of A is lower than B
(b) Pressure on the lower surface of the metal block . pressure on the upper surface of the metal block
Force on the lower surface of the metal block . force on the upper surface of the metal block
A resultant force acts upwards.
This resultant force is the buoyant force.
(c)
$$ \begin{aligned} \text { Weight of block in air } & =m g \\ & =0.050 \times 9.81 \\ & =0.49 \mathrm{~N} \end{aligned} $$
$$ \begin{aligned} & \text { When the metal block is in water: } \\ & \text { Weight of metal block in water }=0.20 \mathrm{~N} \\ & \begin{aligned} \text { Apparent loss in weight of the metal block } & =0.49-0.20 \\ & =0.29 \mathrm{~N} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Buoyant force } & =\text { apparent loss in weight of the metal block } \\ & =0.29 \mathrm{~N} \end{aligned} $$
$$ \begin{aligned} &\text { Buoyant force, } F_{\mathrm{B}}=\rho V g \text {, }\\ &\begin{aligned} & \rho=\text { density of water } \\ & V=\text { volume of water displaced } \\ & \rho V g=0.29 \\ & 1000 \times V \times 9.81=0.29 \\ & V=2.96 \times 10^{-5} \mathrm{~m}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { When the block is in oil: } \\ & \begin{aligned} \text { Volume of oil displaced } & =\text { volume of water displaced } \\ & =2.96 \times 10^{-5} \mathrm{~m}^3 \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Weight of metal block in oil }=0.25 \mathrm{~N} \\ & \begin{aligned} \text { Apparent loss in weight of the metal block } & =0.49-0.25 \\ & =0.24 \mathrm{~N} \end{aligned} \end{aligned} $$
$$ \begin{aligned} \text { Buoyant force } & =\text { apparent loss in weight of the metal block } \\ & =0.24 \mathrm{~N} \end{aligned} $$
$$ \begin{aligned} & \text { Buoyant force, } F_{\mathrm{B}}=\rho V g, \\ & \rho=\text { density of oil } \\ & V=\text { volume of oil displaced } \\ & \quad \rho V g=0.24 \\ & \begin{aligned} \rho \times 2.96 \times 10^{-5} \times 9.81 & =0.24 \\ \quad \rho & =826.5 \mathrm{~kg} \mathrm{~m}^{-3} \end{aligned} \end{aligned} $$
