Question 4:
A laser light beam with a wavelength of 555 nm and a power of 5.00 mW is aimed at an object without any light reflected. Calculate:
(a) the momentum of a photon in the laser beam
(b) the number of photons per second in the laser light beam hitting the object
Answer:
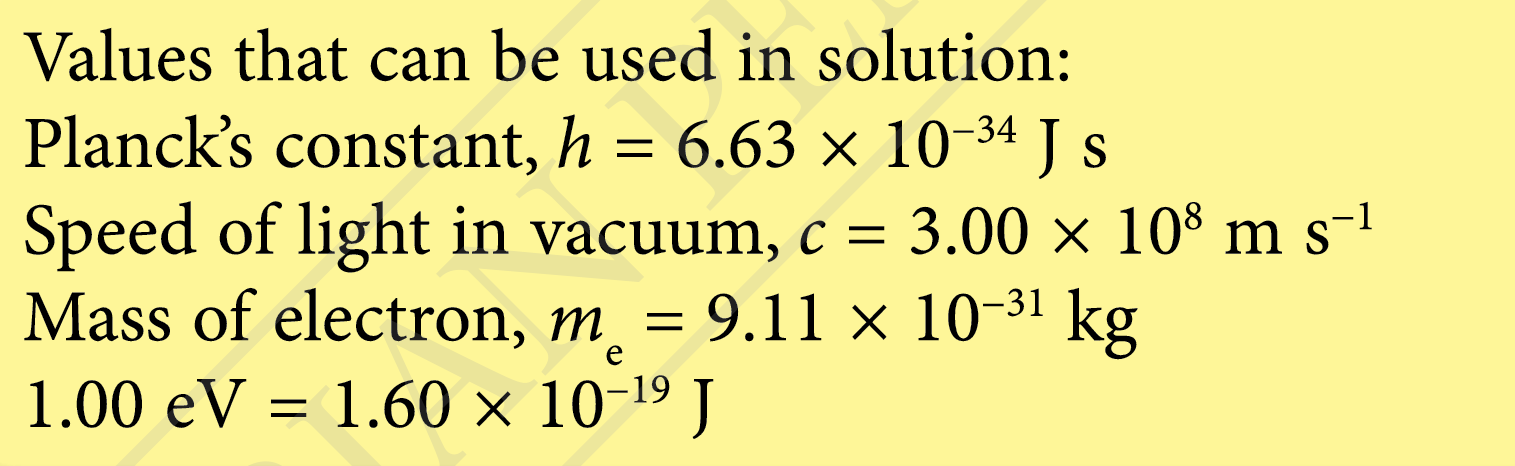
(a)
$$ \begin{aligned} \text { Momentum } & =\frac{h}{\lambda} \\ & =\frac{6.63 \times 10^{-34}}{555 \times 10^{-9}} \\ & =1.19 \times 10^{-27} \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
(b)
$$ \begin{aligned} P & =\frac{n h c}{\lambda} \\ n & =\frac{P \lambda}{h c} \\ & =\frac{\left(5.00 \times 10^{-3}\right)\left(555 \times 10^{-9}\right)}{\left(6.63 \times 10^{-34}\right)\left(3 \times 10^8\right)} \\ & =1.40 \times 10^{16} \mathrm{~s}^{-1} \end{aligned} $$
A laser light beam with a wavelength of 555 nm and a power of 5.00 mW is aimed at an object without any light reflected. Calculate:
(a) the momentum of a photon in the laser beam
(b) the number of photons per second in the laser light beam hitting the object
Answer:
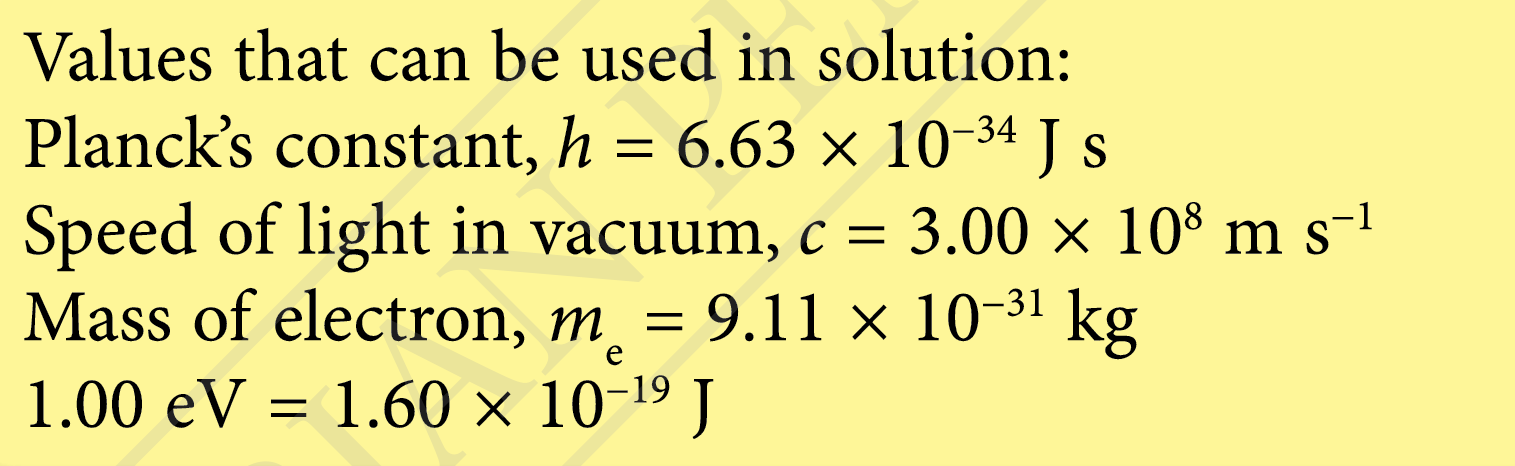
(a)
$$ \begin{aligned} \text { Momentum } & =\frac{h}{\lambda} \\ & =\frac{6.63 \times 10^{-34}}{555 \times 10^{-9}} \\ & =1.19 \times 10^{-27} \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
(b)
$$ \begin{aligned} P & =\frac{n h c}{\lambda} \\ n & =\frac{P \lambda}{h c} \\ & =\frac{\left(5.00 \times 10^{-3}\right)\left(555 \times 10^{-9}\right)}{\left(6.63 \times 10^{-34}\right)\left(3 \times 10^8\right)} \\ & =1.40 \times 10^{16} \mathrm{~s}^{-1} \end{aligned} $$
Question 5:
The de Broglie wavelength of an electron is 1.00 nm.
(a) State Louis de Broglie’s hypothesis of the wave properties of electrons.
(b) Calculate the momentum of the electron.
(c) Calculate the velocity of the electron.
(d) Calculate the kinetic energy of the electron.
Answer:
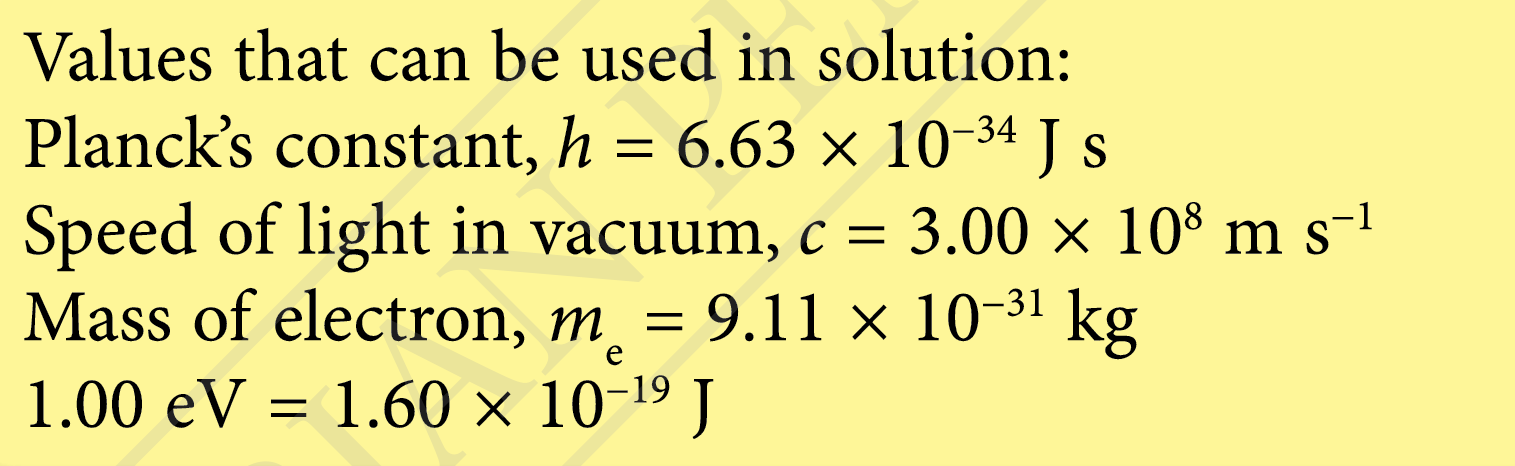
(a)
Louis de Broglie hypothesised that particles such as electrons could have wave properties.
$$ \text { de Broglie wavelength, } \lambda_{\mathrm{e}}=\frac{h}{p} $$
$$ p \text { is the momentum of the electron } $$
(b)
$$ \text { Momentum of the electron, } \begin{aligned} p & =\frac{h}{\lambda} \\ & =\frac{6.63 \times 10^{-34}}{1.00 \times 10^{-9}} \\ & =6.63 \times 10^{-25} \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Velocity of the electron, } v=\frac{p}{m}\\ &\begin{aligned} & =\frac{6.63 \times 10^{-25}}{9.11 \times 10^{-31}} \\ & =7.28 \times 10^5 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} \end{aligned} $$
(d)
$$ \begin{aligned} E & =\frac{1}{2} m v^2 \\ & =\frac{1}{2}\left(9.11 \times 10^{-3}\right)\left(7.28 \times 10^5\right)^2 \\ & =2.41 \times 10^{-19} \mathrm{~J} \end{aligned} $$
The de Broglie wavelength of an electron is 1.00 nm.
(a) State Louis de Broglie’s hypothesis of the wave properties of electrons.
(b) Calculate the momentum of the electron.
(c) Calculate the velocity of the electron.
(d) Calculate the kinetic energy of the electron.
Answer:
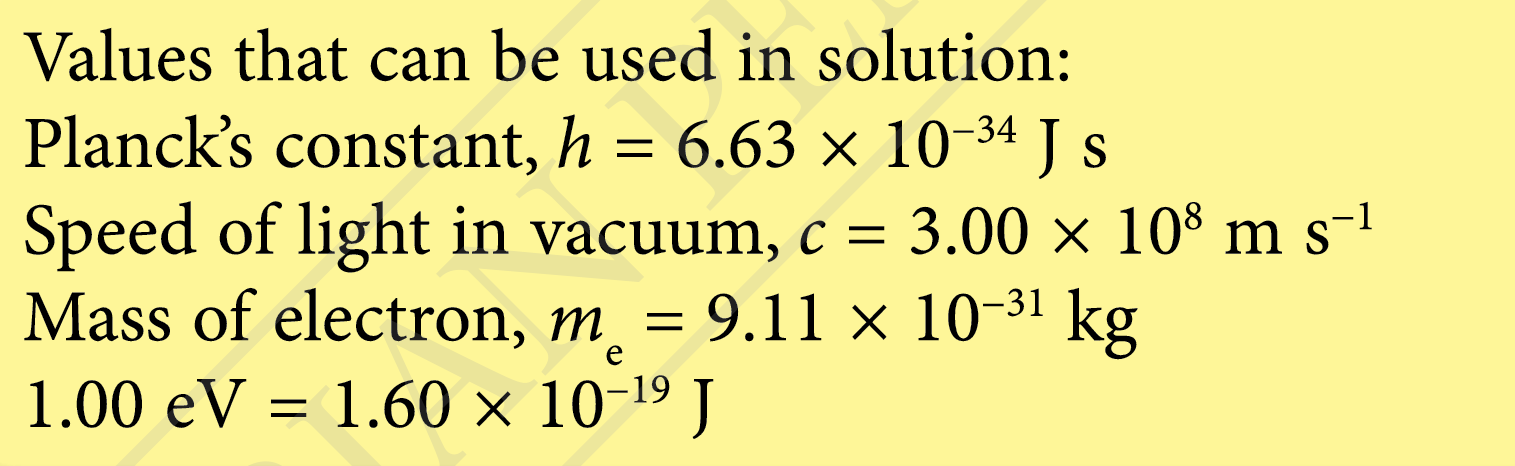
(a)
Louis de Broglie hypothesised that particles such as electrons could have wave properties.
$$ \text { de Broglie wavelength, } \lambda_{\mathrm{e}}=\frac{h}{p} $$
$$ p \text { is the momentum of the electron } $$
(b)
$$ \text { Momentum of the electron, } \begin{aligned} p & =\frac{h}{\lambda} \\ & =\frac{6.63 \times 10^{-34}}{1.00 \times 10^{-9}} \\ & =6.63 \times 10^{-25} \mathrm{~kg} \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} $$
(c)
$$ \begin{aligned} &\text { Velocity of the electron, } v=\frac{p}{m}\\ &\begin{aligned} & =\frac{6.63 \times 10^{-25}}{9.11 \times 10^{-31}} \\ & =7.28 \times 10^5 \mathrm{~m} \mathrm{~s}^{-1} \end{aligned} \end{aligned} $$
(d)
$$ \begin{aligned} E & =\frac{1}{2} m v^2 \\ & =\frac{1}{2}\left(9.11 \times 10^{-3}\right)\left(7.28 \times 10^5\right)^2 \\ & =2.41 \times 10^{-19} \mathrm{~J} \end{aligned} $$
