Question 1:
State the meaning of the following terms:
(a) black body
(b) quantum of energy
Answer:
(a) A black body is an ideal body that is able to absorb all the electromagnetic rays that fall on it.
(b) Quantum of energy is a discrete packet of energy and not a continuous energy.
State the meaning of the following terms:
(a) black body
(b) quantum of energy
Answer:
(a) A black body is an ideal body that is able to absorb all the electromagnetic rays that fall on it.
(b) Quantum of energy is a discrete packet of energy and not a continuous energy.
Question 2:
The minimum energy required for the photoelectron to escape from the sodium metal surface is 2.28 eV .
(a) Will sodium show photoelectric effect for a red light with a wavelength of 680 nm shone on it?
(b) What is the threshold wavelength of sodium?
Answer:
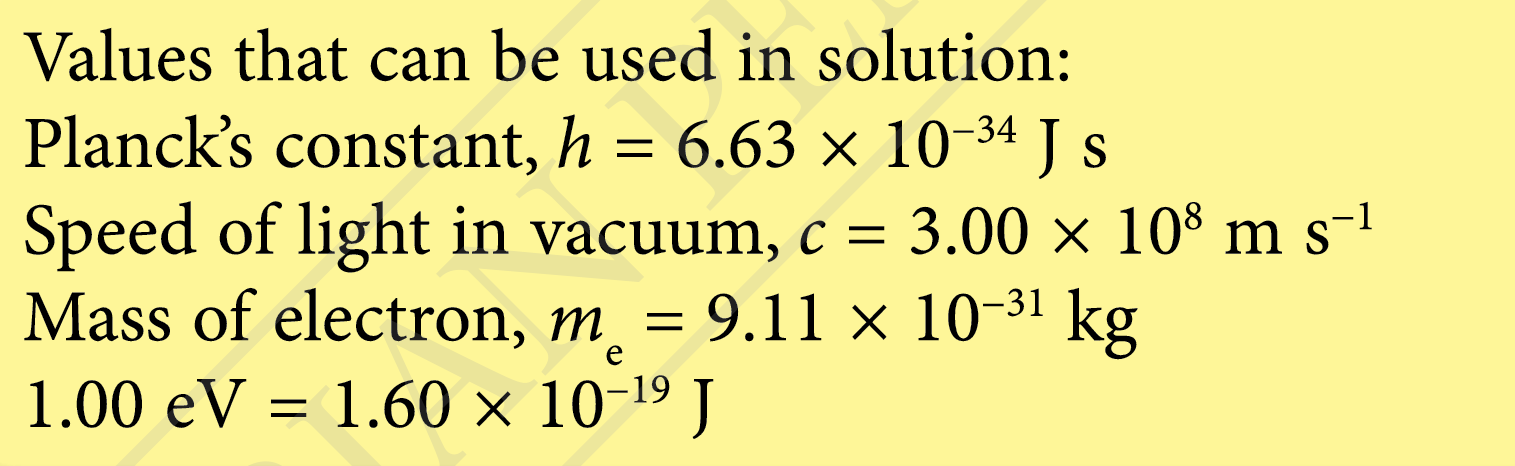
(a)
$$ \begin{aligned} &\text { Work function of sodium metal }\\ &\begin{aligned} & =2.28 \mathrm{eV} \\ & =2.28 \times 1.60 \times 10^{-19} \\ & =3.65 \times 10^{-19} \mathrm{~J} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Photon energy of the red light }\\ &\begin{aligned} & =\frac{h c}{\lambda} \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{680 \times 10^{-9}} \\ & =2.93 \times 10^{-19} \mathrm{~J} \end{aligned} \end{aligned} $$
Photoelectric effect does not occur because of the photon energy of the red light is lower than work function of sodium metal.
(b)
$$ \text { Work function of sodium metal }=\frac{h c}{\lambda_0} $$
$$ \begin{aligned} &\text { Threshold wavelength } \lambda_0\\ &\begin{aligned} & =\frac{h c}{W} \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{3.65 \times 10^{-19}} \\ & =5.45 \times 10^{-7} \mathrm{~m} \\ & =545 \mathrm{~nm} \end{aligned} \end{aligned} $$
The minimum energy required for the photoelectron to escape from the sodium metal surface is 2.28 eV .
(a) Will sodium show photoelectric effect for a red light with a wavelength of 680 nm shone on it?
(b) What is the threshold wavelength of sodium?
Answer:
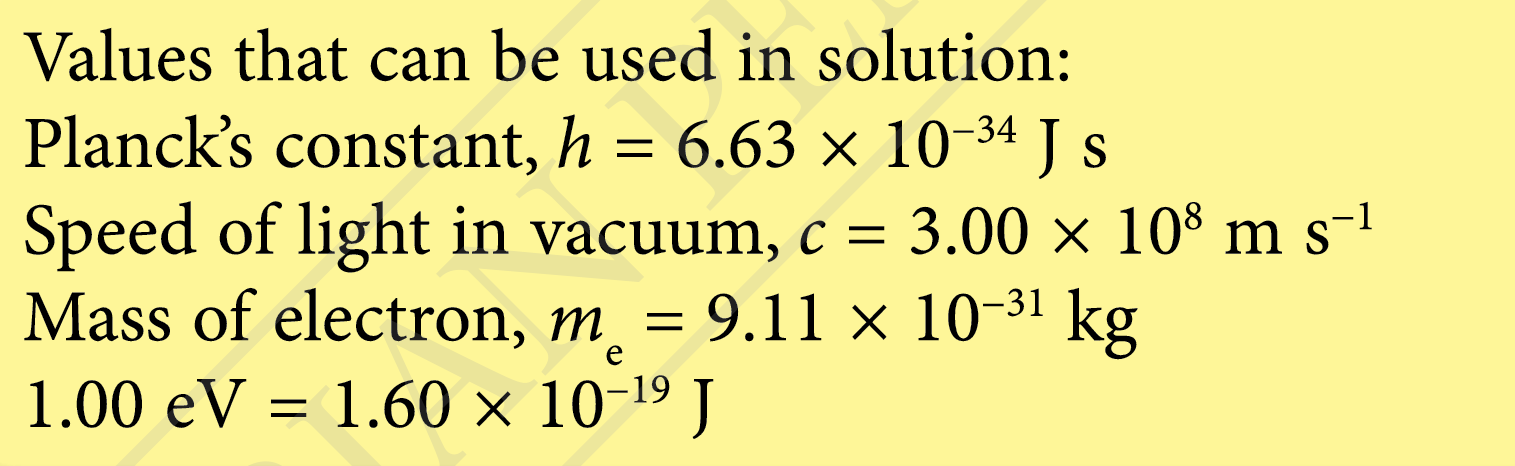
(a)
$$ \begin{aligned} &\text { Work function of sodium metal }\\ &\begin{aligned} & =2.28 \mathrm{eV} \\ & =2.28 \times 1.60 \times 10^{-19} \\ & =3.65 \times 10^{-19} \mathrm{~J} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Photon energy of the red light }\\ &\begin{aligned} & =\frac{h c}{\lambda} \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{680 \times 10^{-9}} \\ & =2.93 \times 10^{-19} \mathrm{~J} \end{aligned} \end{aligned} $$
Photoelectric effect does not occur because of the photon energy of the red light is lower than work function of sodium metal.
(b)
$$ \text { Work function of sodium metal }=\frac{h c}{\lambda_0} $$
$$ \begin{aligned} &\text { Threshold wavelength } \lambda_0\\ &\begin{aligned} & =\frac{h c}{W} \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{3.65 \times 10^{-19}} \\ & =5.45 \times 10^{-7} \mathrm{~m} \\ & =545 \mathrm{~nm} \end{aligned} \end{aligned} $$
Question 3:
Wavelength of the yellow line of the sodium spectrum is 590 nm. How much kinetic energy does one electron have when its de Broglie wavelength is equal to the yellow line of the sodium spectrum?
Answer:
$$ \begin{aligned} &\text { de Broglie wavelength, }\\ &\begin{aligned} \lambda_{\mathrm{e}} & =\frac{h}{p} \\ \lambda_{\mathrm{e}} & =\frac{h}{m V} \\ V & =\frac{h}{m \lambda_{\mathrm{e}}} \\ V & =\frac{6.63 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right)\left(590 \times 10^{-9}\right)} \\ & =1233.51 \mathrm{~ms}^{-1} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Kinetic energy, } K\\ &\begin{aligned} & =\frac{1}{2} m V^2 \\ & =\frac{1}{2}\left(9.11 \times 10^{-31}\right)(1233.51)^2 \\ & =6.93 \times 10^{-25} \mathrm{~J} \end{aligned} \end{aligned} $$
Wavelength of the yellow line of the sodium spectrum is 590 nm. How much kinetic energy does one electron have when its de Broglie wavelength is equal to the yellow line of the sodium spectrum?
Answer:
$$ \begin{aligned} &\text { de Broglie wavelength, }\\ &\begin{aligned} \lambda_{\mathrm{e}} & =\frac{h}{p} \\ \lambda_{\mathrm{e}} & =\frac{h}{m V} \\ V & =\frac{h}{m \lambda_{\mathrm{e}}} \\ V & =\frac{6.63 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right)\left(590 \times 10^{-9}\right)} \\ & =1233.51 \mathrm{~ms}^{-1} \end{aligned} \end{aligned} $$
$$ \begin{aligned} &\text { Kinetic energy, } K\\ &\begin{aligned} & =\frac{1}{2} m V^2 \\ & =\frac{1}{2}\left(9.11 \times 10^{-31}\right)(1233.51)^2 \\ & =6.93 \times 10^{-25} \mathrm{~J} \end{aligned} \end{aligned} $$
