Question 1:
State Pascal’s principle.
Answer:
Pascal’s principle states that the pressure applied on an enclosed fluid is transmitted uniformly in all directions in the fluid.
State Pascal’s principle.
Answer:
Pascal’s principle states that the pressure applied on an enclosed fluid is transmitted uniformly in all directions in the fluid.
Question 2:
Describe how a hydraulic machine can achieve force multiplication by applying Pascal’s principle.
Answer:
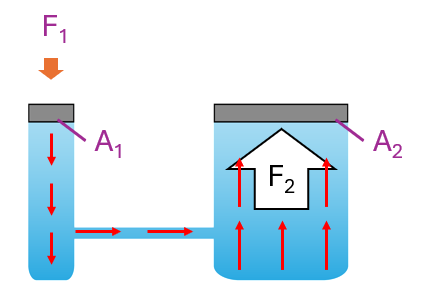
A small force, F1 exerts pressure on the liquid below the small piston.
$$ \text { Pressure }=\frac{F_1}{A_1} $$
$$ \begin{aligned} & A_1=\text { cross-sectional area of the small piston } \\ & A_2=\text { cross-sectional area of the large piston } \end{aligned} $$
According to Pascal’s principle, this pressure is transmitted uniformly throughout the liquid.
$$ \text { This pressure exerts a force } F_2 \text { on the large piston. } $$
$$ \frac{F_2}{A_2}=\frac{F_1}{A_1} \Rightarrow F_2=\frac{F_1}{A_1} \times A_2 $$
$$ \text { Since } A_2>A_1 \text {, thus } F_2>F_1 $$
Therefore, a small input force on the small piston is multiplied to become a larger output force on the large piston.
Describe how a hydraulic machine can achieve force multiplication by applying Pascal’s principle.
Answer:

A small force, F1 exerts pressure on the liquid below the small piston.
$$ \text { Pressure }=\frac{F_1}{A_1} $$
$$ \begin{aligned} & A_1=\text { cross-sectional area of the small piston } \\ & A_2=\text { cross-sectional area of the large piston } \end{aligned} $$
According to Pascal’s principle, this pressure is transmitted uniformly throughout the liquid.
$$ \text { This pressure exerts a force } F_2 \text { on the large piston. } $$
$$ \frac{F_2}{A_2}=\frac{F_1}{A_1} \Rightarrow F_2=\frac{F_1}{A_1} \times A_2 $$
$$ \text { Since } A_2>A_1 \text {, thus } F_2>F_1 $$
Therefore, a small input force on the small piston is multiplied to become a larger output force on the large piston.
Question 3:
In a hydraulic system, an input force of 4.0 N acts on a piston with surface area 0.50 cm2.
Calculate the output force produced on a piston with surface area 6.4 cm2.
Answer:
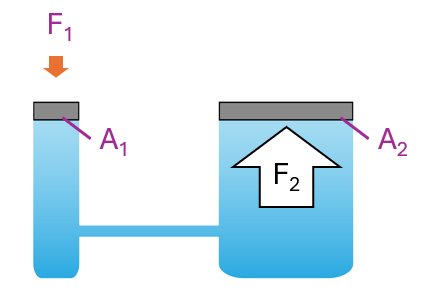
$$ \begin{aligned} & F_1=4.0 \mathrm{~N} \\ & A_1=0.5 \mathrm{~cm}^2 \\ & F_2=? \\ & A_2=6.4 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{gathered} \frac{F_1}{A_1}=\frac{F_2}{A_2} \\ F_2=\frac{A_2}{A_1} \times F_1 \\ F_2=\frac{(6.4)}{(0.50)} \times(4.0) \\ F_2=51.2 \mathrm{~N} \end{gathered} $$
In a hydraulic system, an input force of 4.0 N acts on a piston with surface area 0.50 cm2.
Calculate the output force produced on a piston with surface area 6.4 cm2.
Answer:

$$ \begin{aligned} & F_1=4.0 \mathrm{~N} \\ & A_1=0.5 \mathrm{~cm}^2 \\ & F_2=? \\ & A_2=6.4 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{gathered} \frac{F_1}{A_1}=\frac{F_2}{A_2} \\ F_2=\frac{A_2}{A_1} \times F_1 \\ F_2=\frac{(6.4)}{(0.50)} \times(4.0) \\ F_2=51.2 \mathrm{~N} \end{gathered} $$
Question 4:
A pupil has a small syringe with a piston of diameter 1.5 cm. The pupil intends to construct a hydraulic system that can multiply force from 6 N to 72 N. What is the diameter of a large syringe that is required for this hydraulic system?
Answer:
$$ \begin{aligned} & d_1=1.5 \mathrm{~cm} \\ & F_1=6 \mathrm{~N} \\ & F_2=72 \mathrm{~N} \\ & d_2=? \end{aligned} $$
$$ \begin{aligned} & \frac{F_1}{A_1}=\frac{F_2}{A_2} \\ & A_2=\frac{F_2}{F_1} \times A_1 \\ & A_2=\frac{(72)}{(6)} \times A_1 \\ & A_2=12 A_1 \end{aligned} $$
$$ \begin{aligned} &\text { Surface area }\\ &\begin{aligned} & A=\pi r^2 \\ & A=\pi\left(\frac{d}{2}\right)^2 \\ & A=\frac{\pi \mathrm{d}^2}{4} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Hence, for } A_2=12 A_1 \\ & \frac{\pi d_2^2}{4}=12\left(\frac{\pi d_1^2}{4}\right) \\ & d_2^2=(12) \times(1.5)^2 \\ & d_2=5.20 \mathrm{~cm} \end{aligned} $$
$$ \text { Diameter of large piston }=5.20 \mathrm{~cm} $$
A pupil has a small syringe with a piston of diameter 1.5 cm. The pupil intends to construct a hydraulic system that can multiply force from 6 N to 72 N. What is the diameter of a large syringe that is required for this hydraulic system?
Answer:
$$ \begin{aligned} & d_1=1.5 \mathrm{~cm} \\ & F_1=6 \mathrm{~N} \\ & F_2=72 \mathrm{~N} \\ & d_2=? \end{aligned} $$
$$ \begin{aligned} & \frac{F_1}{A_1}=\frac{F_2}{A_2} \\ & A_2=\frac{F_2}{F_1} \times A_1 \\ & A_2=\frac{(72)}{(6)} \times A_1 \\ & A_2=12 A_1 \end{aligned} $$
$$ \begin{aligned} &\text { Surface area }\\ &\begin{aligned} & A=\pi r^2 \\ & A=\pi\left(\frac{d}{2}\right)^2 \\ & A=\frac{\pi \mathrm{d}^2}{4} \end{aligned} \end{aligned} $$
$$ \begin{aligned} & \text { Hence, for } A_2=12 A_1 \\ & \frac{\pi d_2^2}{4}=12\left(\frac{\pi d_1^2}{4}\right) \\ & d_2^2=(12) \times(1.5)^2 \\ & d_2=5.20 \mathrm{~cm} \end{aligned} $$
$$ \text { Diameter of large piston }=5.20 \mathrm{~cm} $$
