Question 6:
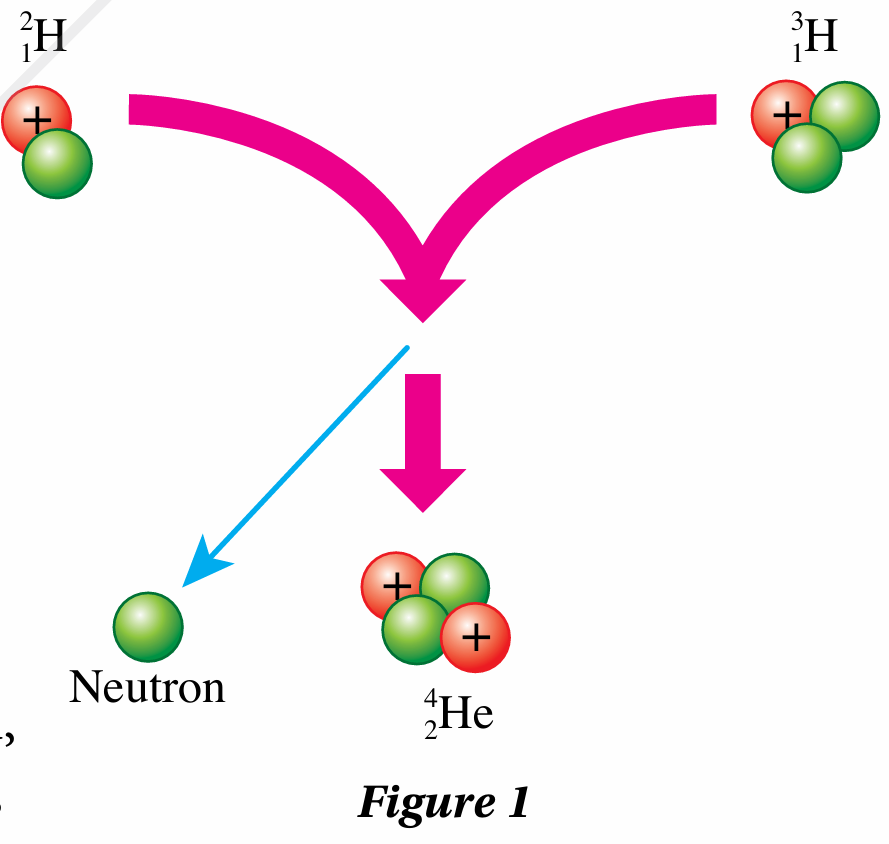
In a nuclear reaction as shown in Figure 1, the total mass of the particles that are produced is less than the initial mass of the particles. The nuclear reaction experiences a mass defect. The lost mass is converted into energy.
(a) Name the nuclear reaction and write the equation involved.
(b) Calculate the mass defect and the nuclear energy that is released.
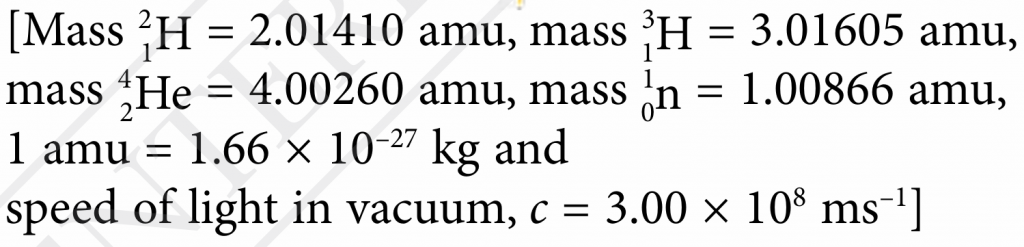
Answer:
(a)
(b)
$$ \text { Masss defect, } \begin{aligned} m & =(2.01410+3.01605)-(4.00260+1.00866) \\ & =0.01889 \text { amu } \end{aligned} $$
$$ \text { Masss defect, } \begin{aligned} m(\text { in unit kg) } & =0.01889 \times 1.66 \times 10^{-27} \\ & =3.1357 \times 10^{-29} \mathrm{~kg} \end{aligned} $$

In a nuclear reaction as shown in Figure 1, the total mass of the particles that are produced is less than the initial mass of the particles. The nuclear reaction experiences a mass defect. The lost mass is converted into energy.
(a) Name the nuclear reaction and write the equation involved.
(b) Calculate the mass defect and the nuclear energy that is released.
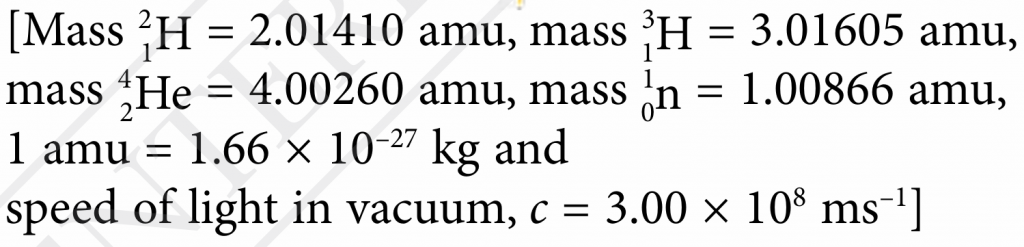
Answer:
(a)
Nuclear fusion
$$ { }_1^2 \mathrm{H}+{ }_1^3 \mathrm{H} \rightarrow{ }_2^4 \mathrm{He}+{ }_0^1 \mathrm{n}+\text { energy } $$(b)
$$ \text { Masss defect, } \begin{aligned} m & =(2.01410+3.01605)-(4.00260+1.00866) \\ & =0.01889 \text { amu } \end{aligned} $$
$$ \text { Masss defect, } \begin{aligned} m(\text { in unit kg) } & =0.01889 \times 1.66 \times 10^{-27} \\ & =3.1357 \times 10^{-29} \mathrm{~kg} \end{aligned} $$
The nuclear energy that is released,
$$ \begin{aligned} E & =m c^2 \\ & =3.1357 \times 10^{-29} \times\left(3.00 \times 10^8\right)^2 \\ & =2.82 \times 10^{-12} \mathrm{~J} \end{aligned} $$Question 7:
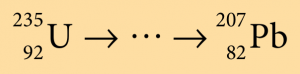
A radioactive decay series of a source of uranium-235 is
(a) What is the number of α-particles and β-particles emitted?
(b) Draw a graph of the nucleon number against atomic number that is possible for the decay series.
Answer:
(a)
$$ { }_{92}^{235} \mathrm{U} \rightarrow{ }_{82}^{207} \mathrm{~Pb}+x{ }_2^4 \mathrm{He}+y{ }_{-1}^0 e $$
$$ \begin{aligned} 235 & =207+4 x+0 \\ 235-207 & =4 x \\ 28 & =4 x \\ x & =\frac{28}{4} \\ & =7 \alpha-\text { particles } \end{aligned} $$
$$ \begin{aligned} 92 & =82+2 x-y \\ 92 & =82+2(7)-y \\ y & =82+14-92 \\ y & =4 \beta-\text { particles } \end{aligned} $$
(b)
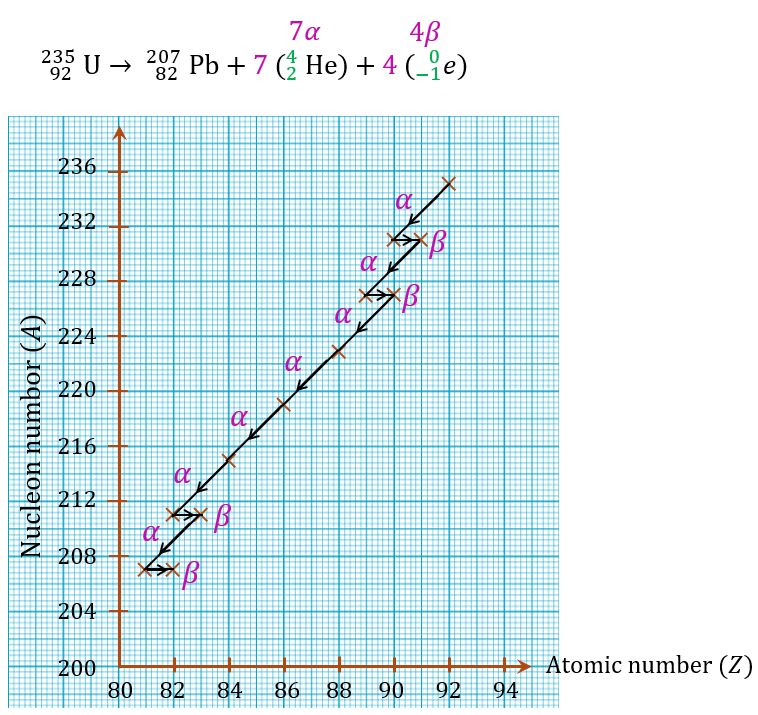
A radioactive decay series of a source of uranium-235 is

(a) What is the number of α-particles and β-particles emitted?
(b) Draw a graph of the nucleon number against atomic number that is possible for the decay series.
Answer:
(a)
$$ { }_{92}^{235} \mathrm{U} \rightarrow{ }_{82}^{207} \mathrm{~Pb}+x{ }_2^4 \mathrm{He}+y{ }_{-1}^0 e $$
$$ \begin{aligned} 235 & =207+4 x+0 \\ 235-207 & =4 x \\ 28 & =4 x \\ x & =\frac{28}{4} \\ & =7 \alpha-\text { particles } \end{aligned} $$
$$ \begin{aligned} 92 & =82+2 x-y \\ 92 & =82+2(7)-y \\ y & =82+14-92 \\ y & =4 \beta-\text { particles } \end{aligned} $$
Thus, 7 α-particles and 4 β-particles are emitted.
(b)

