Question 1:
(a) Derive the formula for pressure at depth h in a liquid with density ρ.
(b) Calculate the pressure at depth of 24 m in a lake that contains water with a density of 1 120 kg m–3.
[Gravitational acceleration, g = 9.81 m s–2]
Answer:
(a)
Consider a liquid column in a container
Height of liquid column = h
Area of the base of liquid column = A
Density of liquid = ρ
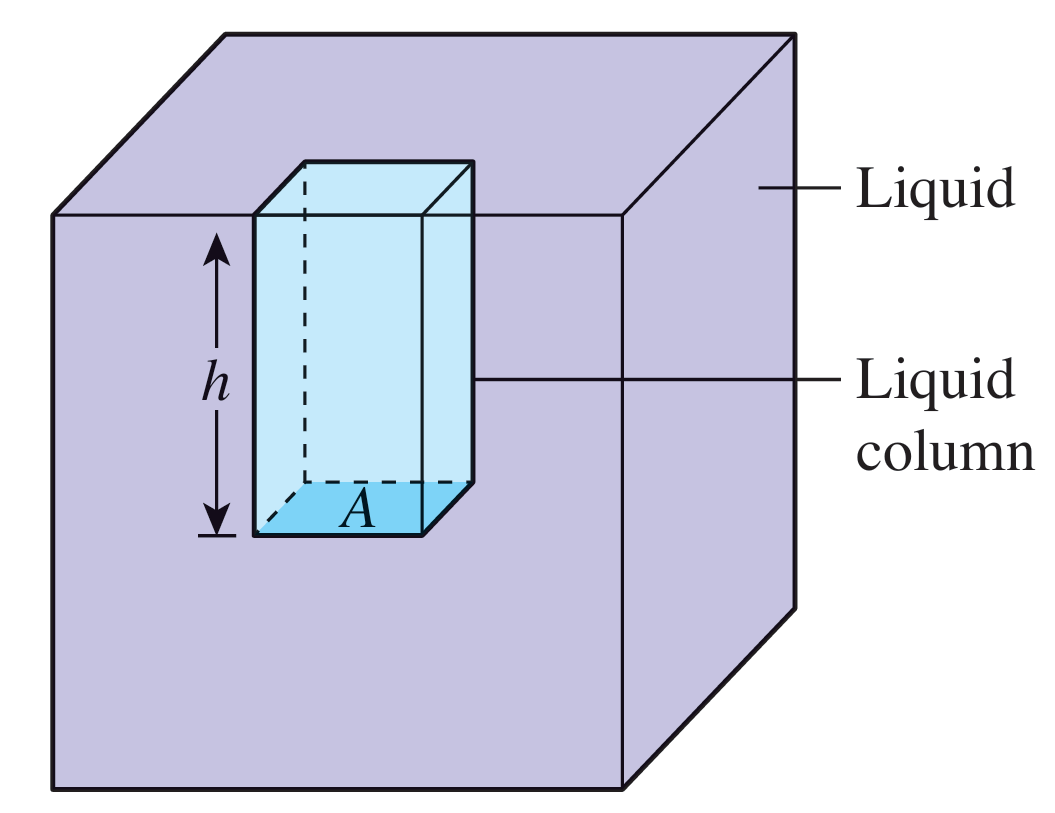
Pressure on the base of the liquid column is due to the weight of the liquid column.
Volume of liquid column, V = Ah
Mass of liquid column, m = Ahρ
Weight of liquid column, W = Ahρg
$$ \begin{aligned} &\text { Pressure on the base of liquid column, }\\ &\begin{aligned} & P=\frac{\text { Weight of liquid column }}{\text { Surface area }} \\ & P=\frac{A h \rho g}{A} \\ & P=h \rho g \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} P & =h \rho g \\ & =24 \times 1120 \times 9.81 \\ & =2.64 \times 10^5 \mathrm{~Pa} \end{aligned} $$
(a) Derive the formula for pressure at depth h in a liquid with density ρ.
(b) Calculate the pressure at depth of 24 m in a lake that contains water with a density of 1 120 kg m–3.
[Gravitational acceleration, g = 9.81 m s–2]
Answer:
(a)
Consider a liquid column in a container
Height of liquid column = h
Area of the base of liquid column = A
Density of liquid = ρ

Pressure on the base of the liquid column is due to the weight of the liquid column.
Volume of liquid column, V = Ah
Mass of liquid column, m = Ahρ
Weight of liquid column, W = Ahρg
$$ \begin{aligned} &\text { Pressure on the base of liquid column, }\\ &\begin{aligned} & P=\frac{\text { Weight of liquid column }}{\text { Surface area }} \\ & P=\frac{A h \rho g}{A} \\ & P=h \rho g \end{aligned} \end{aligned} $$
(b)
$$ \begin{aligned} P & =h \rho g \\ & =24 \times 1120 \times 9.81 \\ & =2.64 \times 10^5 \mathrm{~Pa} \end{aligned} $$
Question 2:
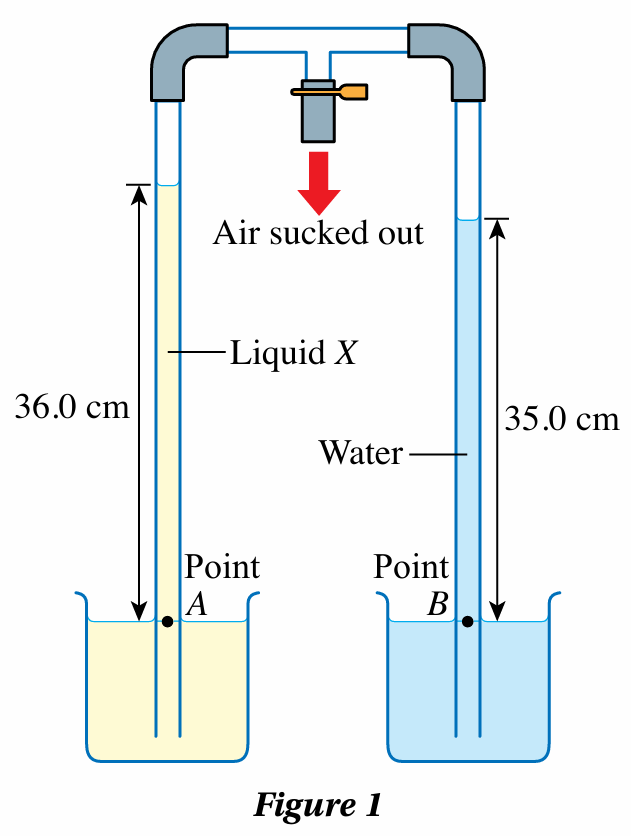
Figure 1 shows the apparatus for comparing the densities of two types of liquid after some air is sucked out of the apparatus.
(a) Explain why the pressure at point A is equal to the pressure at point B.
(b) Calculate the density of liquid X.
[Density of water, ρ = 1 000 kg m–3]
Answer:
(a)
A and B are at the same level in a stationary liquid.
(b)
$$ \text { Density of liquid } X=\rho $$
$$ \begin{aligned} \text { Pressure at } A & =\text { pressure at } B \\ 36.0 \times \rho \times g & =35.0 \times 1000 \times g \\ \rho & =972 \mathrm{~kg} \mathrm{~m}^{-3} \end{aligned} $$

Figure 1 shows the apparatus for comparing the densities of two types of liquid after some air is sucked out of the apparatus.
(a) Explain why the pressure at point A is equal to the pressure at point B.
(b) Calculate the density of liquid X.
[Density of water, ρ = 1 000 kg m–3]
Answer:
(a)
A and B are at the same level in a stationary liquid.
(b)
$$ \text { Density of liquid } X=\rho $$
$$ \begin{aligned} \text { Pressure at } A & =\text { pressure at } B \\ 36.0 \times \rho \times g & =35.0 \times 1000 \times g \\ \rho & =972 \mathrm{~kg} \mathrm{~m}^{-3} \end{aligned} $$
Question 3:
Compare and contrast the existence of pressure in the liquids and the atmospheric pressure.
Answer:
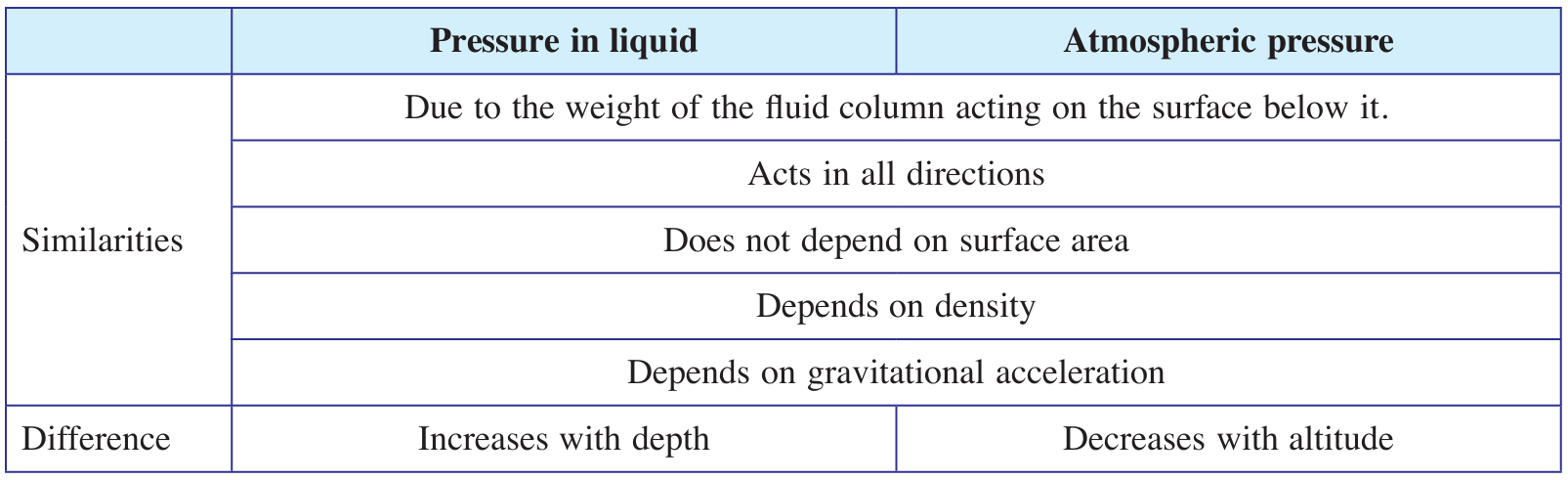
Compare and contrast the existence of pressure in the liquids and the atmospheric pressure.
Answer:

