Question 4:
Figure 2 shows a U-tube containing mercury.
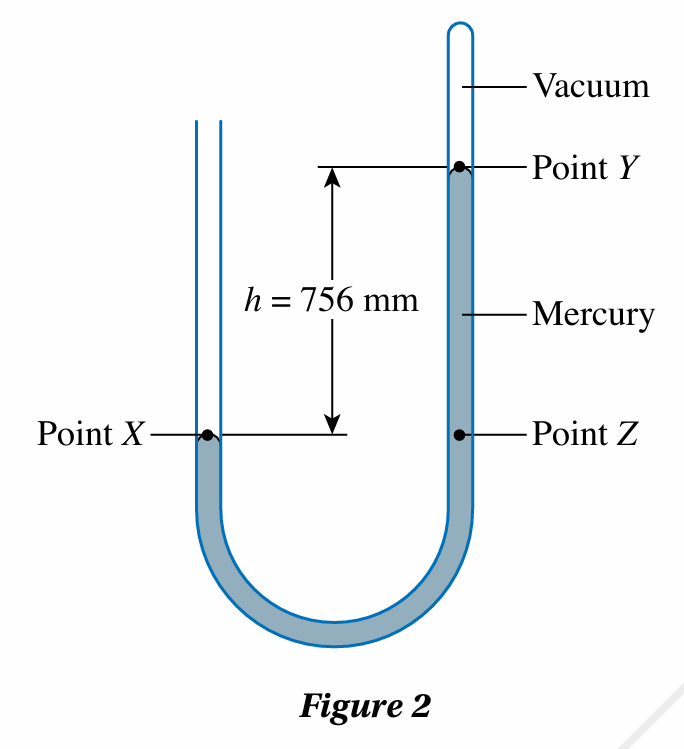
(a) What is the pressure acting on point X and point Y on the surface of mercury?
(b) By comparing the pressure at point X and point Z, explain why the height of the mercury column, h is a measure of atmospheric pressure.
(c) Determine the atmospheric pressure in Pa.
[Density of mercury, ρ = 13 600 kg m–3 and gravitational acceleration, g = 9.81 m s–2]
Answer:
(a)
Pressure at point X = atmospheric pressure
Pressure at point Y = 0
(b)
Since point X and point Z are at the same level,
Pressure at point X = pressure at point Z
Pressure at point X = atmospheric pressure, and
Pressure at point Z = pressure due to mercury column + 0
Atmospheric pressure = pressure due to mercury column
Therefore, the height of the mercury column, h is a measure of atmospheric pressure.
(c) $$ \begin{aligned} \text { Atmospheric pressure } & =756 \mathrm{~mm} \mathrm{Hg}=0.756 \mathrm{~m} \mathrm{Hg} \\ \text { Atmospheric pressure } & =0.756 \times 13600 \times 9.81 \\ & =100862 \mathrm{~Pa} \end{aligned} $$
Figure 2 shows a U-tube containing mercury.

(a) What is the pressure acting on point X and point Y on the surface of mercury?
(b) By comparing the pressure at point X and point Z, explain why the height of the mercury column, h is a measure of atmospheric pressure.
(c) Determine the atmospheric pressure in Pa.
[Density of mercury, ρ = 13 600 kg m–3 and gravitational acceleration, g = 9.81 m s–2]
Answer:
(a)
Pressure at point X = atmospheric pressure
Pressure at point Y = 0
(b)
Since point X and point Z are at the same level,
Pressure at point X = pressure at point Z
Pressure at point X = atmospheric pressure, and
Pressure at point Z = pressure due to mercury column + 0
Atmospheric pressure = pressure due to mercury column
Therefore, the height of the mercury column, h is a measure of atmospheric pressure.
(c) $$ \begin{aligned} \text { Atmospheric pressure } & =756 \mathrm{~mm} \mathrm{Hg}=0.756 \mathrm{~m} \mathrm{Hg} \\ \text { Atmospheric pressure } & =0.756 \times 13600 \times 9.81 \\ & =100862 \mathrm{~Pa} \end{aligned} $$
Question 5:
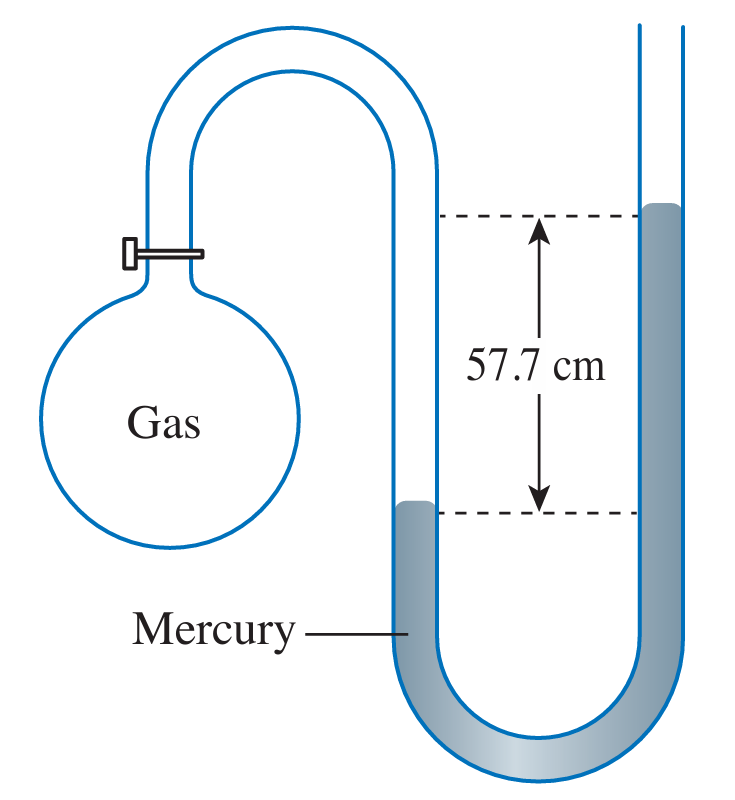
A mercury manometer is connected to a cylinder containing gas. The gas pressure in the cylinder and the atmospheric pressure are 180 kPa and 103 kPa respectively.
Sketch a diagram of the manometer connected to the gas cylinder. Determine the height of the mercury column in your sketch.
[Density of mercury, ρ = 13 600 kg m–3 and gravitational acceleration, g = 9.81 m s–2]
Answer:
Difference between the pressure of the compressed air and atmospheric pressure
$$ \begin{aligned} & =180-103 \\ & =77 \mathrm{kPa} \\ & =77000 \mathrm{~Pa} \end{aligned} $$
$$ \begin{aligned} h \rho g & =77000 \\ h \times 13600 \times 9.81 & =77000 \\ h & =0.577 \mathrm{~m} \\ h & =57.7 \mathrm{~cm} \end{aligned} $$
Difference in height between the two mercury columns in the manometer = 57.7 cm
A mercury manometer is connected to a cylinder containing gas. The gas pressure in the cylinder and the atmospheric pressure are 180 kPa and 103 kPa respectively.
Sketch a diagram of the manometer connected to the gas cylinder. Determine the height of the mercury column in your sketch.
[Density of mercury, ρ = 13 600 kg m–3 and gravitational acceleration, g = 9.81 m s–2]
Answer:
Difference between the pressure of the compressed air and atmospheric pressure
$$ \begin{aligned} & =180-103 \\ & =77 \mathrm{kPa} \\ & =77000 \mathrm{~Pa} \end{aligned} $$
$$ \begin{aligned} h \rho g & =77000 \\ h \times 13600 \times 9.81 & =77000 \\ h & =0.577 \mathrm{~m} \\ h & =57.7 \mathrm{~cm} \end{aligned} $$
Difference in height between the two mercury columns in the manometer = 57.7 cm

Question 6:
In a hydraulic brake system, the driver of the vehicle applies a force of 80 N on the brake pedal. This force is multiplied by the mechanical lever system to be a 400 N input force on the hydraulic liquid in the master cylinder. The diameter of the master cylinder and the diameter of the slave cylinder are 0.8 cm and 2.5 cm respectively.
(a) Calculate the pressure on the hydraulic liquid in the master cylinder.
(b) State the principle that enables pressure to be transmitted from the master cylinder to the slave cylinder.
(c) What is the braking force produced at the slave cylinder to stop the rotation of the wheel?
RRRRRRRRRRRR
Answer:
(a)
$$ \begin{aligned} & \text { Diameter of master cylinder }=0.8 \mathrm{~cm} \\ & \text { Cross-sectional area of master cylinder }=\frac{\pi \times 0.8^2}{4} \\ &=0.50 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Pressure } & =\frac{400}{0.50} \\ & =800 \mathrm{~N} \mathrm{~cm}^{-2} \end{aligned} $$
(b) Pascal’s principle
(c)
$$ \begin{aligned} \text { Cross-sectional area of slave cylinder } & =\frac{\pi \times 2.5^2}{4} \\ & =4.91 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Braking force } & =\text { pressure } \times \text { surface area } \\ & =800 \times 4.91 \\ & =3928 \mathrm{~N} \end{aligned} $$
In a hydraulic brake system, the driver of the vehicle applies a force of 80 N on the brake pedal. This force is multiplied by the mechanical lever system to be a 400 N input force on the hydraulic liquid in the master cylinder. The diameter of the master cylinder and the diameter of the slave cylinder are 0.8 cm and 2.5 cm respectively.
(a) Calculate the pressure on the hydraulic liquid in the master cylinder.
(b) State the principle that enables pressure to be transmitted from the master cylinder to the slave cylinder.
(c) What is the braking force produced at the slave cylinder to stop the rotation of the wheel?
RRRRRRRRRRRR
Answer:
(a)
$$ \begin{aligned} & \text { Diameter of master cylinder }=0.8 \mathrm{~cm} \\ & \text { Cross-sectional area of master cylinder }=\frac{\pi \times 0.8^2}{4} \\ &=0.50 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Pressure } & =\frac{400}{0.50} \\ & =800 \mathrm{~N} \mathrm{~cm}^{-2} \end{aligned} $$
(b) Pascal’s principle
(c)
$$ \begin{aligned} \text { Cross-sectional area of slave cylinder } & =\frac{\pi \times 2.5^2}{4} \\ & =4.91 \mathrm{~cm}^2 \end{aligned} $$
$$ \begin{aligned} \text { Braking force } & =\text { pressure } \times \text { surface area } \\ & =800 \times 4.91 \\ & =3928 \mathrm{~N} \end{aligned} $$
