Question 1:
(a) State Einstein’s Photoelectric Equation.
(b) State the meaning of:
(i) work function
(ii) threshold frequency
(iii) the relationship between work function and threshold frequency
Answer:
(a)
$$ h f=W+\frac{1}{2} m v^2 \text { max } $$
(b)(i)
Work function, W is the minimum energy required for a photoelectron to be emitted from a metal surface.
(b)(ii)
Threshold frequency, f0 is the minimum frequency for a light photon to produce photoelectric effect.
(b)(iii)
W = hf0
(a) State Einstein’s Photoelectric Equation.
(b) State the meaning of:
(i) work function
(ii) threshold frequency
(iii) the relationship between work function and threshold frequency
Answer:
(a)
$$ h f=W+\frac{1}{2} m v^2 \text { max } $$
(b)(i)
Work function, W is the minimum energy required for a photoelectron to be emitted from a metal surface.
(b)(ii)
Threshold frequency, f0 is the minimum frequency for a light photon to produce photoelectric effect.
(b)(iii)
W = hf0
Question 2:
(a) Sketch a graph to show the relationship between the maximum kinetic energy of photoelectrons and the frequency of light shone on a metal.
(b) What are the physical quantities represented by the gradient and the intercepts of the graph sketched in 2(a)?
Answer:
(a)
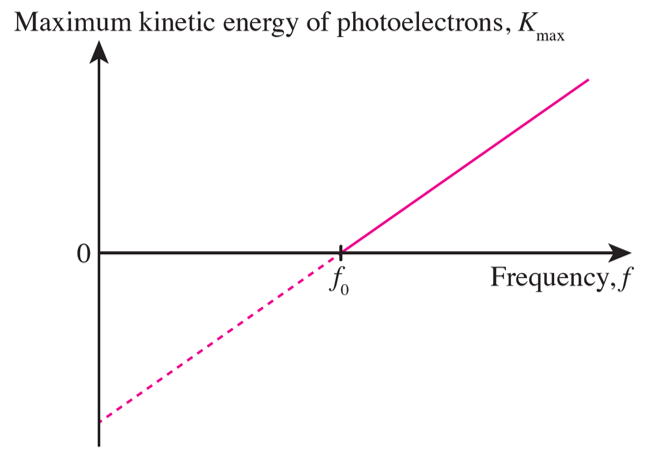
(b)
Gradient of the graph = Planck’s constant, h
Graph intercept on the frequency axis = threshold frequency of the metal, f0
Graph intercept on the Kmax axis = work function of the metal, W
(a) Sketch a graph to show the relationship between the maximum kinetic energy of photoelectrons and the frequency of light shone on a metal.
(b) What are the physical quantities represented by the gradient and the intercepts of the graph sketched in 2(a)?
Answer:
(a)

(b)
Gradient of the graph = Planck’s constant, h
Graph intercept on the frequency axis = threshold frequency of the metal, f0
Graph intercept on the Kmax axis = work function of the metal, W
Question 3:
When a metal with a work function of 4.32 × 10–19 J is shone on by a violet light (λ = 4 × 10–7 m), what is the maximum kinetic energy of an emitted photoelectron?
[Planck’s constant, h = 6.63 × 10–34 J s, speed of light in vacuum, c = 3.00 × 108 m s–1]
Answer:
$$ \text { Work function, } W=4.32 \times 10^{-19} \mathrm{~J} $$
$$ \text { Wavelength, } \lambda=4 \times 10^{-7} \mathrm{~m} $$
$$ \text { Planck’s constant, } h=6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s} $$
$$ \text { Speed of light in vacuum, } c=3.00 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1} $$
$$ \begin{aligned} h f & =W+K_{\text {max }} \\ h\left(\frac{c}{\lambda}\right) & =W+K_{\text {max }} \\ K_{\text {max }} & =\frac{h c}{\lambda}-W \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{4 \times 10^{-7}}-4.32 \times 10^{-19} \\ & =6.53 \times 10^{-20} \mathrm{~J} \end{aligned} $$
When a metal with a work function of 4.32 × 10–19 J is shone on by a violet light (λ = 4 × 10–7 m), what is the maximum kinetic energy of an emitted photoelectron?
[Planck’s constant, h = 6.63 × 10–34 J s, speed of light in vacuum, c = 3.00 × 108 m s–1]
Answer:
$$ \text { Work function, } W=4.32 \times 10^{-19} \mathrm{~J} $$
$$ \text { Wavelength, } \lambda=4 \times 10^{-7} \mathrm{~m} $$
$$ \text { Planck’s constant, } h=6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s} $$
$$ \text { Speed of light in vacuum, } c=3.00 \times 10^8 \mathrm{~m} \mathrm{~s}^{-1} $$
$$ \begin{aligned} h f & =W+K_{\text {max }} \\ h\left(\frac{c}{\lambda}\right) & =W+K_{\text {max }} \\ K_{\text {max }} & =\frac{h c}{\lambda}-W \\ & =\frac{\left(6.63 \times 10^{-34}\right)\left(3.00 \times 10^8\right)}{4 \times 10^{-7}}-4.32 \times 10^{-19} \\ & =6.53 \times 10^{-20} \mathrm{~J} \end{aligned} $$
